所有效率之和等于零。
1
2
3
4
5
6
7
| public static void solve() {
int n = io.nextInt(), sum = 0;
for (int i = 0; i < n - 1; i++) {
sum += io.nextInt();
}
io.println(-sum);
}
|
贪心选择最小花费的通知,注意维护已经被通知的下标,根据该下标判断是否需要加 \(p\),并且如果某个人通知其他人的成本大于 \(p\),则他不会通知其他人。发现大佬的解法好简单,取一个最小值,维护一个剩余人数即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| public static void solve() {
int n = io.nextInt(), p = io.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = io.nextInt();
}
int[] b = new int[n];
for (int i = 0; i < n; i++) {
b[i] = io.nextInt();
}
var aux = new Integer[n];
for (int i = 0; i < n; i++) {
aux[i] = i;
}
Arrays.sort(aux, (i, j) -> b[i] - b[j]);
long ans = p;
int r = n - 1;
for (int i : aux) {
int x = Math.min(r, a[i]);
ans += (long) x * Math.min(p, b[i]);
r -= x;
}
io.println(ans);
}
|
分类讨论,注意被 \(n\) 整除的数。
1
2
3
4
5
6
7
| public static void solve() {
int n = io.nextInt(), m = io.nextInt(), k = io.nextInt();
if (k == 3) io.println(Math.max(0, m - n - m / n + 1));
else if (k == 2) io.println(m / n + Math.min(n - 1, m));
else if (k == 1) io.println(1);
else io.println(0);
}
|
很容易的想到计算选择每个索引位置,能够得到的最大分数,时间复杂度为 \(O(n\log{n})\)。然后计算每个位置有多少种方案,比赛时我以为选择一个索引位置,默认就选择了它的所有倍数位置,导致不会做。其实只要排序,然后每个位置的方案数就是它左边的数选或不选的方案数,这样可以保证不会重复计算,所以快速幂计算方案数(可以在遍历的时候计算方案数),再乘以得分累加到答案即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| private static final int MOD = 998244353;
public static void solve() {
int n = io.nextInt();
int[] dp = new int[n + 1];
for (int i = 1; i <= n; i++) {
dp[i] = io.nextInt();
}
dp[0] = Integer.MAX_VALUE;
for (int i = 1; i <= n; i++) {
for (int j = 2 * i; j <= n; j += i) {
dp[i] = Math.max(dp[i], dp[j]);
}
}
Arrays.sort(dp);
long ans = 0L, pow = 1L;
for (int i = 0; i < n; i++) {
ans = (ans + dp[i] * pow) % MOD;
pow = pow * 2 % MOD;
}
io.println(ans);
}
|
方法一:内向基环树
对于每个 \(i\),建立一条从 \(i\) 指向 \(a_{i}\) 的边,最终会得到多个内向基环树。规则一:入度为零的节点不会被选择;规则二:如果一个节点的所有入度节点都被选择,那么它不会被选择;规则三:如果一个节点不被选择,那么它指向的节点会被选择。(以上规则可以使用拓扑序 + 染色法实现)
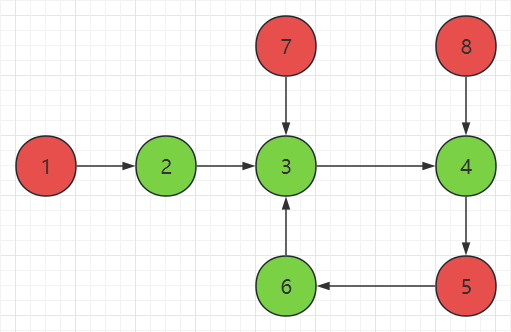
如图,数组为 \([2,3,4,5,6,3,3,4]\),剩余索引 \([1,5,7,8]\),剩余元素 \([2,6,3,4]\),选择索引 \([2,6,3,4]\)。应用规则一,得出索引 \([1,7,8]\) 不被选择;应用规则三,得出索引 \([2,3,4]\) 被选择;应用规则二,得出索引 \([5]\) 不被选择;应用规则三,得出索引 \([6]\) 被选择。
特殊情况,如果内向基环树没有环外节点,无法应用上述规则,那么需要单独对环交替染色,若此时环的长度为奇数,则没有解,其他情况均有解。也就是说,当且仅当内向基环树没有环外节点,且环的长度为奇数时,无解。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| public static void solve() {
int n = io.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = io.nextInt() - 1;
}
int[] in = new int[n];
for (int i = 0; i < n; i++) {
in[a[i]]++;
}
int[] col = new int[n];
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < n; i++) {
if (in[i] == 0) {
q.offer(i);
col[i] = -1;
}
}
while (!q.isEmpty()) {
int x = q.poll(), y = a[x];
if (col[y] != 0) continue;
if (--in[y] == 0 || col[x] == -1) {
q.offer(y);
col[y] = -col[x];
}
}
for (int i = 0; i < n; i++) {
if (col[i] != 0) continue;
int j = i, pre = -1;
while (col[j] == 0) {
col[j] = -pre;
pre = col[j];
j = a[j];
}
if (col[j] == pre) {
io.println(-1);
return;
}
}
List<Integer> ans = new ArrayList<>();
for (int i = 0; i < n; i++) {
if (col[i] == -1) ans.add(a[i] + 1);
}
io.println(ans.size());
for (int x : ans) {
io.print(x + " ");
}
io.println();
}
|
方法二:外向基环树
好像有建立外向基环树的解法,没时间看,在此。
