发表更新基础 / 系统20 分钟读完 (大约2975个字)

System Design（草稿）

参考 GitHub Awesome System Design。

短链系统

我的想法

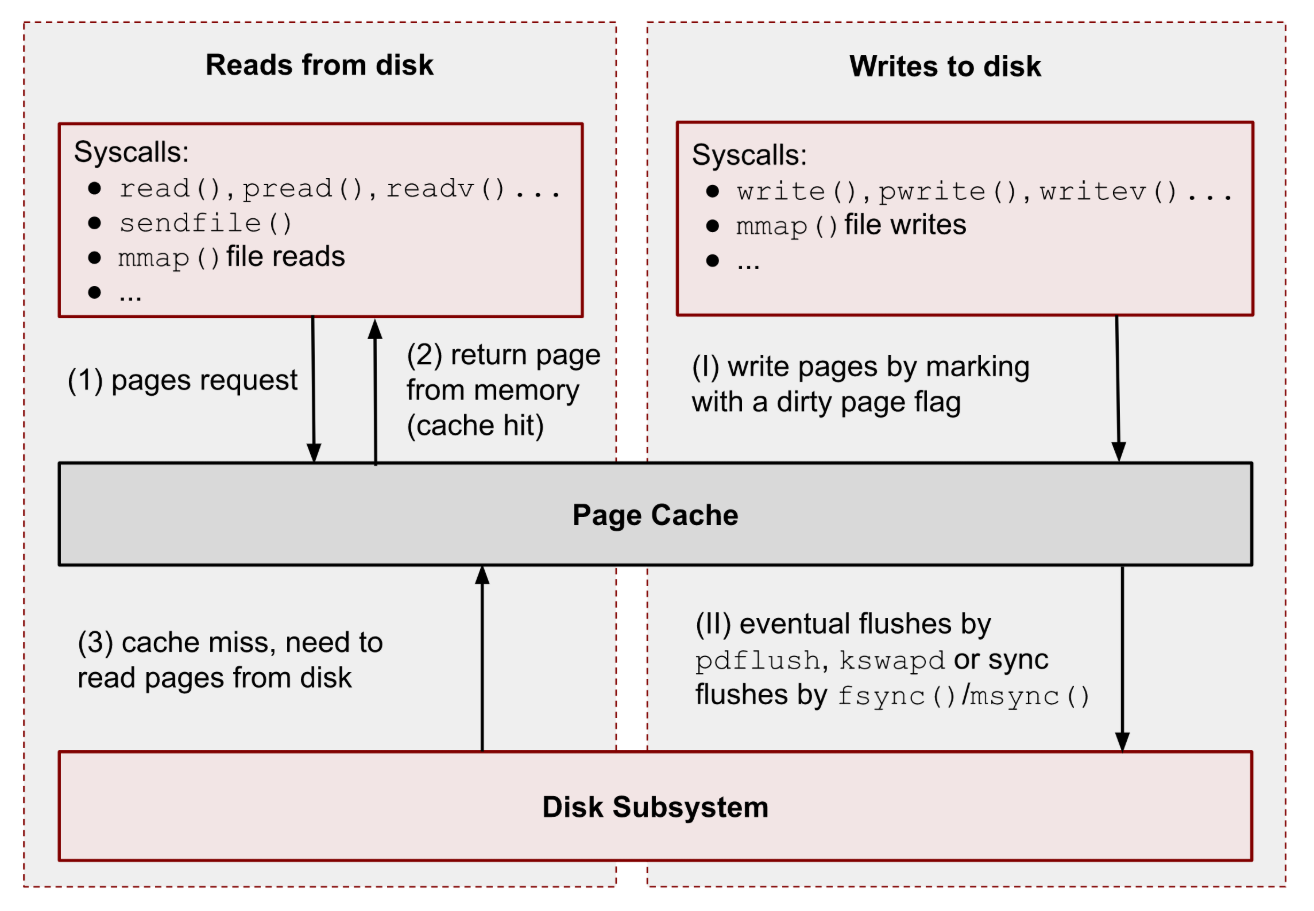
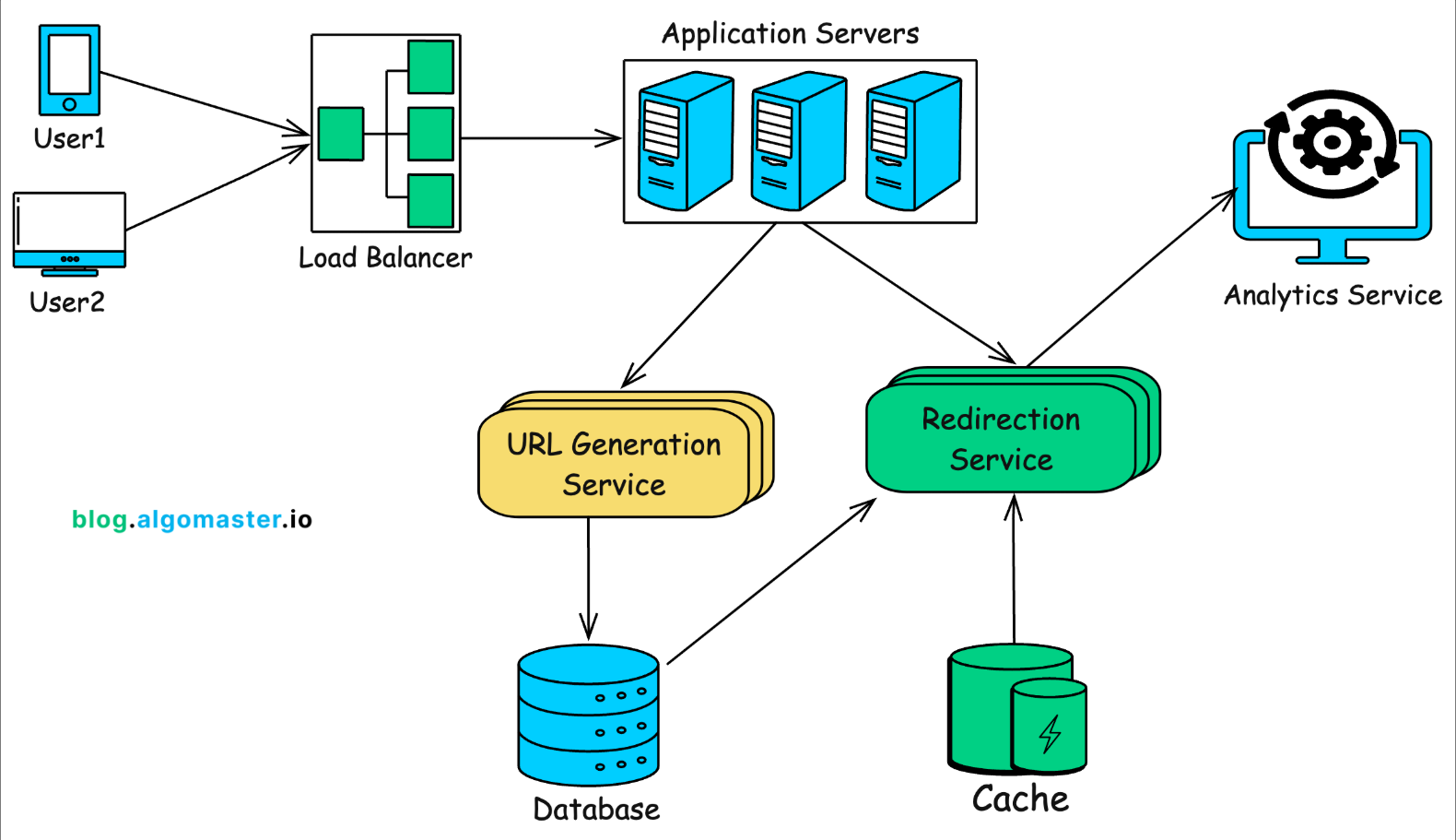
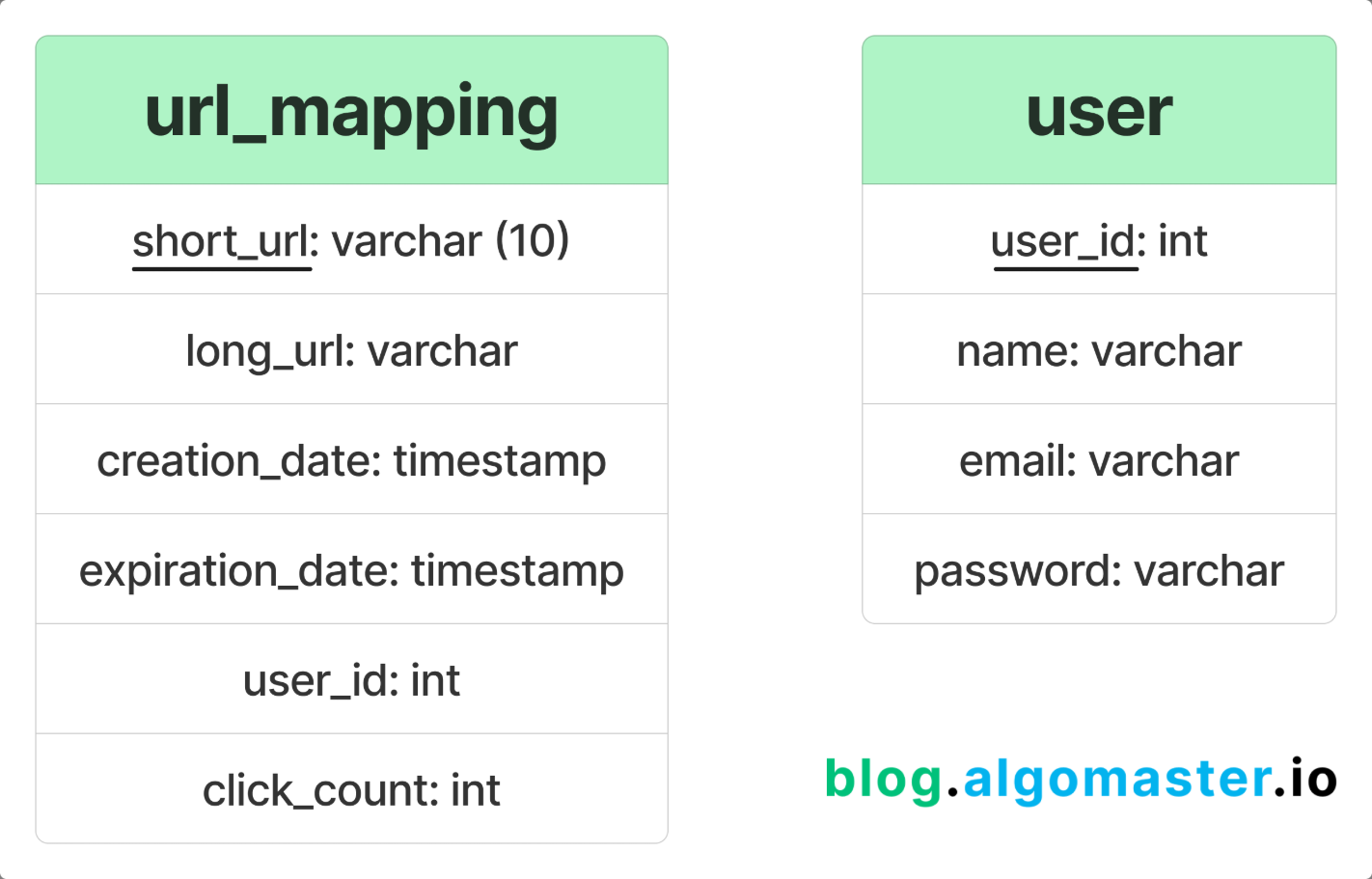
核心功能就是长链转短链，可以从使用算法和存储方式两个方面思考。算法首先想到的是哈希函数，可以将长链转为一个短链整数（需要处理哈希冲突），然后使用 Base62 编码为包含 [0-9a-zA-z] 的短链字符串。存储时可以存储长链和短链整数/字符串，不同存储格式主要是时间和空间的权衡，然后需要分别在两个字段上建立唯一/前缀索引来加速查询。

实际上可以将数据库的主键 ID 作为短链整数，这样空间占用更小，也不存在哈希冲突。查询短链到长链的映射可以直接利用主键索引，只需给长链建立索引来加速反向查询。虽然每次查询都要将短链整数编码为短链字符串，不过时间开销不算大，长度为 7 的字符串就可以表示 \(62^7\approx3\times 10^{12}\) 个不同的短链，而且可以使用缓存提升查询性能。

文章内容

需求分析可以分为功能性需求和非功能性需求，功能性需求主要是业务需求，非功能性需求包括高性能、高可用、可扩展性和安全性。然后可以假设流量特征来估算系统的吞吐量、磁盘/内存空间以及带宽需求。流量特征可以从每日缩短 URL 的请求数量、读写比例、峰值流量和平均 URL 长度等方面思考。最后根据估算结果来估计需要的基础设施。

假设每天 100 万个缩短 URL 的请求，读写比例 100 : 1，峰值流量是平均负载的 10 倍，平均 URL 长度为 100 个字符。计算吞吐量，平均写吞吐量 \(\frac{\times 10^{6}}{24\times3600}\approx 12\) WPS，平均读吞吐量 \(100\times 12=1200\) RPS。假设每个 URL 占用 127 字节的存储空间，由短链 7 字节、长链 100 字节、创建时间 8 字节、到期时间 8 字节和点击次数 4 字节组成，那么每年就需要 \(127\times 10^{6}\times 365\approx 46.4\) GB 的磁盘存储空间。假设读取返回的 HTTP 301 重定向大小为 500 字节，每天读取带宽为 \(500\times 10^{6}\times 100= 50\) GB/day，每秒峰值读取带宽为 \(500\times RPS\times 10= 6\) MB/s。

系统负载是读多写少的，假设负载符合二八定律（Pareto principle），即 20% 的 URL 产生 80% 的读取流量。假设每天缓存 20% 的 URL，则需要 \(127\times 10^{6}\times 0.2=25.4\) MB 的内存作为缓存。假设缓存命中率为 90%，则到达数据库的平均请求数量为 \(1200\times0.1=120\) RPS。最后根据以上估算结果，估计使用 4-6 个服务器，每个服务器能够处理 200~300 RPS，10~20 个分布式数据库节点，3~4 个分布式缓存节点。

由于需要存储数十亿条记录，而且数据库操作大多是简单的键值查找，不需要执行复杂的表连接，所以选择使用 DynamoDB 或 Cassandra 等 NoSQL 数据库，因为它们能够高效处理数十亿次简单键值的查找，而且提供高可扩展性和高可用性。

可以对长链使用哈希函数（MD5、SHA-256）得到哈希值，然后取哈希值的前缀转十进制，再使用 Base64 编码得到短链。要处理哈希冲突，可以使用不同的种子重新哈希或者取哈希值的其它位生成短链，也可以将增量后缀附加到短链。另一种生成短链的方式是使用分布式 ID（数据库自增 ID、Redis 生成 ID、雪花算法），从安全性角度思考，增量 ID 是可预测的，有人可以通过使用短链服务推断系统的 URL 总数或者猜测其他用户生成的 URL，混淆（Obfuscation）增量 ID 可以缓解该问题。

额外功能：① 用户自定义短链，需要进行格式校验以及唯一性检查，如果和已有的短链发生冲突，服务器可以返回错误或者建议的替换方案。服务器还可以保留部分短链，以供内部使用。② 设置短链的过期时间，由用户指定或者使用默认的过期时间，可以使用定时任务或者在请求时检测短链是否过期，然后（逻辑）删除过期短链。③ 可以使用消息队列记录短链的访问日志，然后批量处理日志将其聚合存储在数据仓库中，以实现分析服务。

其他问题：① 使用负载均衡、基于范围/哈希的分片、缓存保证可扩展性。② 使用复制、自动故障转移、跨多个地理区域部署服务保证可用性。③ 处理边界条件，例如对于过期短链服务器返回 HTTP 401 状态码，不存在的短链返回 404 状态码，在生成短链时检测冲突。④ 限流防止滥用，输入校验确保用户提供的短链不包含恶意内容，使用 HTTPS 防止窃听和中间人攻击，对异常活动模式进行监控和报警。

遗漏的点

功能性需求没有想到重定向和过期时间的设计，以及允许用户自定义短链、数据分析等额外功能。重定向可以使用 301/302 状态码（永久/临时重定向），临时重定向每次请求都会经过短链服务，从而可以统计短链的使用次数。没有特别思考非功能性需求，基本上是从单服务器的角度思考问题。对哈希函数有点误解，误认为哈希的结果都是整数，像是 MD5、SHA 生成的哈希值都是可以包含字母的。我之前都是默认使用 MySQL + Redis 的组合，没有想到使用其他 NoSQL 数据库。使用哈希函数索引实现长链快速判重，使用布隆过滤器过滤请求。

一些疑问

Q：为什么估计使用 4-6 个服务器，10~20 个分布式数据库节点，3~4 个分布式缓存节点？

Q：文章描述的系统似乎只会检测短链冲突，而没有检测重复的长链？

Q：DynamoDB 和 Cassandra 数据库有什么特点？

排行榜系统

我的想法

排行榜主要是按照分数对用户进行排序，功能性需求主要是显示排名和更新排名。像是游戏打完排位会显示排名上升多少，然后排行榜只会显示 TopK 用户，每隔固定时间才更新榜单。像是算法比赛的排行榜会显示所有用户，榜单也是实时更新的。对于 TopK 榜单一般会使用小顶堆来实现，当新分数大于堆顶元素时，就弹出堆顶元素然后将当前元素入堆。

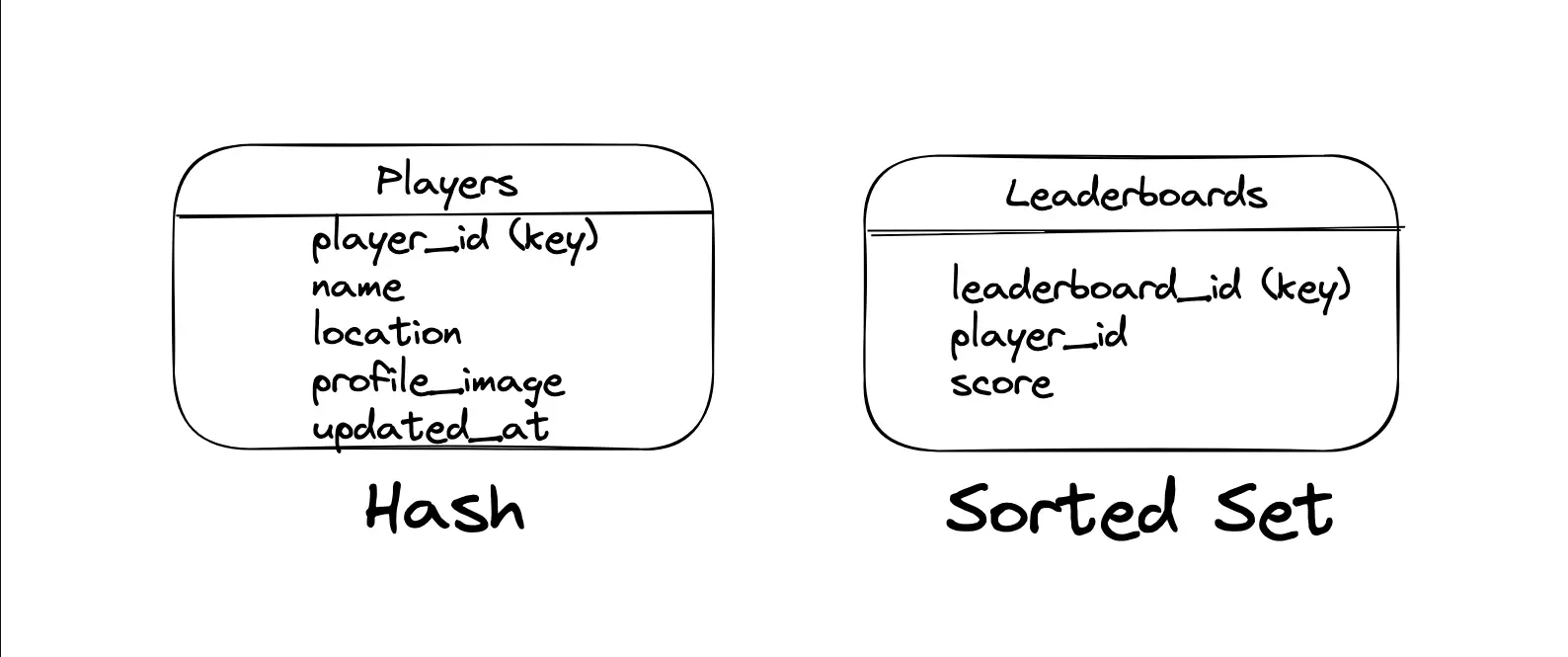
那么其他用户如何在分数变化之后计算排名呢？简单的想法就是直接更新 MySQL 数据库中的分数，然后获取所有小于该分数的用户数量。对于游戏这种分数频繁变化的场景，更新、查询数据库的磁盘 I/O 开销较大。如果能够将所有用户的分数信息缓存到 Redis 中，则可以直接使用跳表维护排行榜，然后使用消息队列异步更新数据库（类似后写缓存策略）。

像是算法比赛这种结束之后排名就不会变化的场景，数据库中也可以存储排名信息（而不只是分数）。如果内存中存不下所有用户的分数信息，可以对数据分片使用多个 Redis 节点维护排行榜，获取排名就需要对所有节点数据做聚合。应该也可以使用统计数据估算排名，返回给前端的是估算排名而不是真正的排名，然后后台使用定时任务去修正排名。

文章内容

排行榜分为绝对排行榜和相对排行榜，绝对排行榜显示 TopK 用户，相对排行榜显示指定用户周围的用户。HTTP 响应可以设置 cache-control: private, no-cache, must-revalidate, max-age=5 使用缓存，状态码 202 表示异步处理请求、401 表示身份未认证、403 表示没有权限，使用 HEAD 请求查看服务的健康状况。

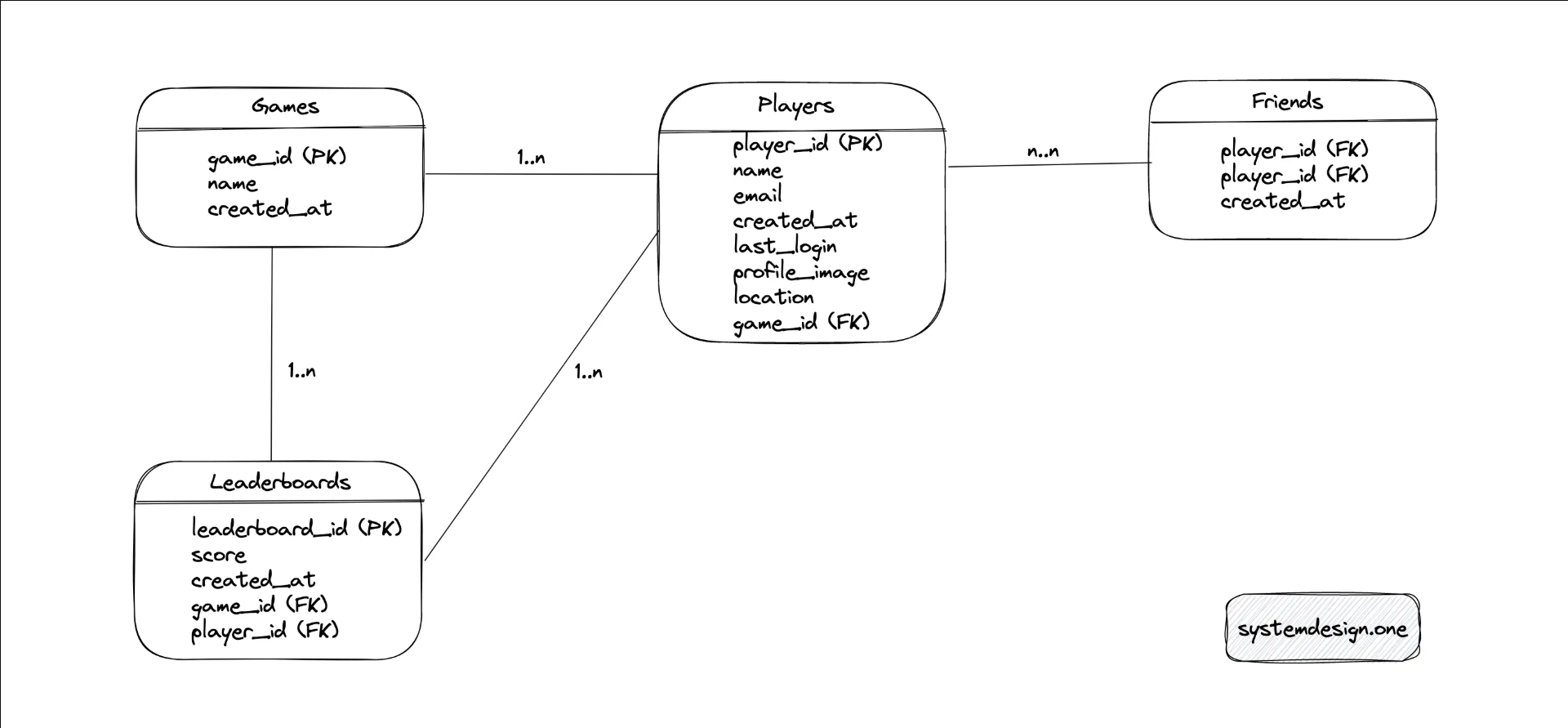
功能性需求：绝对和相对排行榜，可以查看指定用户的排名，排行榜可以划分为全球、区域和朋友圈，可以查看历史比赛的排行榜，可以根据每天/周/月的游戏情况进行排名，客户端以分布式的方式在全球范围内更新排行榜。流量特征：每天 5000 万个写入请求，读写比例为 5 : 1，用户分布在全球各地，排行榜需实时显示。

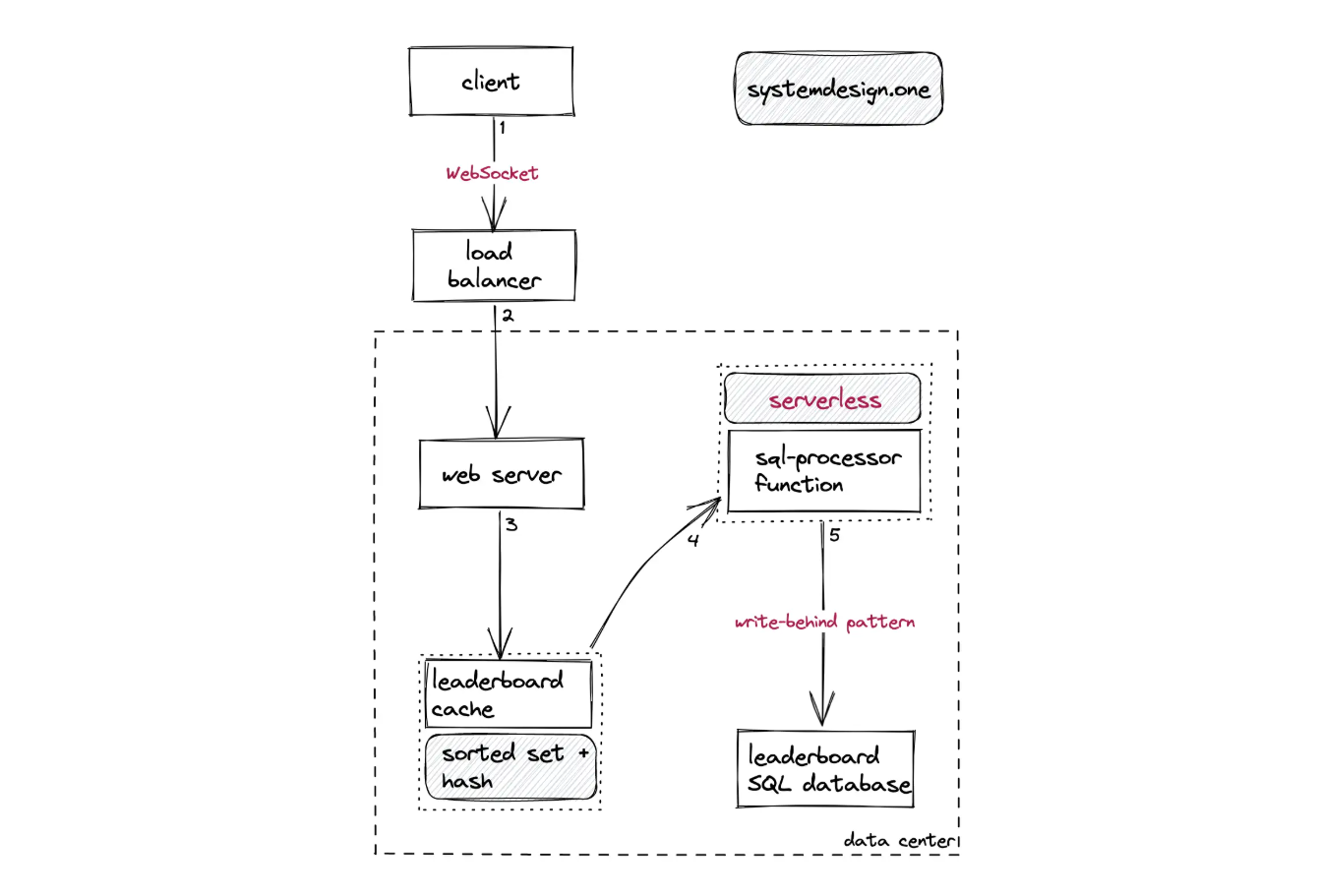
客户端使用 WebSocket 协议和负载均衡器建立连接，保证排行榜的实时性（允许服务器主动推送数据）。依然使用 DynamoDB 实现可扩展性，将玩家 ID 作为分区键、玩家得分作为排序键。东西有点多，看得有点懵，先实现再说。

遗漏的点

单个用户的分数变化会导致其他用户的排名也发生变化（导致缓存失效），所以使用 MySQL 数据库获取排名的方式需要全表扫描更新所有用户的排名，或者延迟更新每个用户的排名，磁盘 I/O 开销会比我之前想的更大。更新 MySQL 分数之后应该主动更新缓存而不是删除缓存（从 Cache Aside 变为类似 Write Through），确保所有用户都在 Redis 的排行榜中（所以也不能设置过期时间），避免重建整个排行榜。不过主动更新缓存可能导致不一致，例如网络原因导致缓存更新失败、并发更新的顺序交错导致旧数据覆盖新数据，可以使用消息队列排队、重试请求保证正确性。

一些疑问

Q：既然游戏和用户的关系是一对多，即不同游戏的用户不会共享，那么完全没有必要将不同游戏的数据耦合到一个数据库中。而且 Redis 维护的排行榜数据以 leaderboard_id 作为键是有问题的，这可是 Leaderboards 表的主键。

发表更新基础 / 模板12 分钟读完 (大约1765个字)

快速傅里叶变换（FFT）

参考 Reducible。

问题

如何求两个 \(n\) 次多项式 \(A(x)\) 和 \(B(x)\) 的乘积 \(C(x)\)？最简单的方式是使用乘法分配律对每个系数做乘积，时间复杂度为 \(O(n^{2})\)。

$$ A(x)=a_{0}+a_{1}x^{1}+\cdots+a_{n-1}x^{n} \\ B(x)=b_{0}+b_{1}x^{1}+\cdots+b_{n-1}x^{n} \\ C(x)=c_{0}+c_{1}x^{1}+\cdots+c_{2n}x^{2n} $$

另一种想法是：① 在多项式 \(A(x)\) 和 \(B(x)\) 上取 \(2n+1\) 个点 \(x_{i}\)，其中 \(i=0,1,\cdots,2n\)，求出对应的函数值。② 根据 \(C({x_{i}})=A(x_{i})\cdot B(x_{i})\)，可以得到 \(C(x)\) 上的 \(2n+1\) 个点。③ 使用拉格朗日插值，化简得到 \(C(x)\) 的表达式。总时间复杂度为 \(O(n^{2})\)，如果能够将 ① 和 ③ 的时间复杂度优化为 \(O(n\log{n})\)，那么就能够降低总时间复杂度。

优化步骤 ①

可以发现，对于偶函数 \(f(x)=f(-x)\)，对于奇函数 \(f(x)=-f(-x)\)。如果将多项式分解为偶函数和奇函数两部分，则可以可以利用对称性快速求点值。不妨设 \(n\) 为偶数，将 \(n-1\) 次多项式 \(P(x)\) 划分为偶函数和奇函数两部分。

$$ \begin{align}P(x)&=p_{0}+p_{1}x^{1}+\cdots+p_{n-1}x^{n-1} \\&=(p_{0}+p_{2}x^{2}+\cdots+p_{n-2}x^{n-2})+(p_{1}+p_{3}x^{3}+\cdots+p_{n-1}x^{n-1}) \\&=(p_{0}+p_{2}x^{2}+\cdots+p_{n-2}x^{n-2})+x(p_{1}+p_{3}x^{2}+\cdots+p_{n-1}x^{n-2})\end{align} $$

设 \(P_{e}(x)=p_{0}+p_{2}x^{1}+\cdots+p_{n-2}x^{\frac{n}{2}-2}\)，\(P_{o}(x)=p_{1}+p_{3}x^{2}+\cdots+p_{n-1}x^{\frac{n}{2}-2}\)，则 \(P(x)=P_{e}(x^{2})+xP_{o}(x^{2})\)。此时，如果取 \(n\) 个点 \(\pm x_{0},\pm x_{1},\cdots,\pm x_{\frac{n}{2}-1}\)，则只需要计算 \(P_{e}(x_{i}^{2})\) 和 \(P_{o}(x_{i}^{2})\)，就能够通过以下方式得到两个函数值。

$$ P(x_{i})=P_{e}(x_{i}^{2})+x_{i}P_{o}(x_{i}^{2}) \\ P(-x_{i})=P_{e}(x_{i}^{2})-x_{i}P_{o}(x_{i}^{2}) $$

所以，要求 \(P(x)\) 上的 \(n\) 个点值，等价于求 \(P_{e}(x^{2})\) 和 \(P_{o}(x^{2})\) 上的 \(\frac{n}{2}\) 个点值，即点 \(x_{0},x_{1},\cdots,x_{\frac{n}{2}-1}\) 的值。此时，原问题被分解为两个相同的子问题，并且子问题的大小只有原问题的一半，如果子问题能够按照原问题的方式继续分解，则可以得到时间复杂度为 \(O(n\log{n})\) 的算法。

但是，\(P_{e}(x^{2})\) 和 \(P_{o}(x^{2})\) 不能继续分解，因为定义域 \(x^{2}\geq 0\)，点 \(x_{0}^{2},x_{1}^{2},\cdots,x_{\frac{n}{2}-1}^{2}\) 不构成正负对，也就不能利用对称性求点值。如果能够取到一组构成正负对的点，在子问题中所有正点依然构成正负对，那么就可以继续递推。此时，需要引入复数，例如，取点 \(\pm 1,\pm i\) 构成正负对，子问题中 \(1^{2},i^{2}\) 等价于 \(1,-1\) 依然构成正负对。

那么对于 \(n-1\) 次多项式，如何取满足条件的 \(n\) 个点？假设取某个点 \(z\)，那么必然要取 \(-z\)，在子问题中 \(z\) 变为 \(z^{2}\)，那么必然要取 \(-z^{2}\)，以此类推，假设 \(n\) 为 \(2\) 的幂（总是可以通过对高次项补系数 \(0\) 取到），则最终得到 \(z^{n}\)。也就是说，所有取值的 \(n\) 次方都相等，不妨设 \(z^{n}=1\)，求解方程可以得到 \(n\) 个单位根，即为满足条件的 \(n\) 个点。

设复数 \(z=a+bi\)，则极坐标表示为 \(z=r(cos(\varphi)+isin(\varphi))\)，根据欧拉公式，有 \(z=re^{\varphi i}\)。要求 \(z^{n}=1\)，即求 \(r^{n}e^{\varphi ni}=e^{2k\pi i}\)，得出 \(r=1,\varphi =\frac{2k\pi}{n}\)，所以 \(z=e^{\frac{2k\pi}{n}i}\)，其中 \(k=0,1,\cdots,n-1\)。设 \(w_{n}=e^{\frac{2\pi}{n}i}\)，则 \(n\) 个单位根分别为 \(w_{n}^{0},w_{n}^{1},\cdots,w_{n}^{n-1}\)，它们将复平面中的单位圆 \(n\) 等分。

观察单位根的性质，有 \(w_{n}^{k}=-w_{n}^{k+\frac{n}{2}}\)，\(w_{n}^{k}=w_{\frac{n}{2}}^{\frac{k}2}\)，所以 \(w_{n}^{0},w_{n}^{1},\cdots,w_{n}^{\frac{n}{2}-1}\) 和 \(w_{n}^{\frac{n}{2}},w_{n}^{\frac{n}{2}+1},\cdots,w_{n}^{n-1}\) 构成正负对。在子问题中，\(w_{n}^{0},w_{n}^{1},\cdots,w_{n}^{\frac{n}{2}-1}\) 变为 \(w_{n}^{0},w_{n}^{2},\cdots,w_{n}^{n-2}\)，等价于 \(w_{\frac{n}{2}}^{0},w_{\frac{n}{2}}^{1},\cdots,w_{\frac{n}{2}}^{\frac{n}{2}-1}\)，前半和后半依然构成正负对，以此类推。从复平面的角度思考，更容易理解。

根据上述讨论，单位根的正负对性质，在所有子问题中都成立，所以求 \(n-1\) 次多项式 \(P(x)\) 的 \(n\) 个点值，可以使用递归分治的方式求解。当 \(n=1\) 时，多项式是常数，\(P(w_{1}^{0})\) 就是该常数值。当 \(n>1\) 时，如果已知 \(P_{e}(x^{2})\) 和 \(P_{o}(x^{2})\) 在 \(w_{n}^{k}\) 的点值，其中 \(k<\frac{n}{2}\)，则利用之前推出的 \(P(x)=P_{e}(x^{2})+xP_{o}(x^{2})\) 公式可以得到以下两个函数值。

$$ P(w_{n}^{k}) =P_{e}(w_{n}^{2k})+w_{n}^{k}P_{o}(w_{n}^{2k}) \\ P(-w_{n}^{k}) =P(w_{n}^{k+\frac{n}{2}}) =P_{e}(w_{n}^{2k+n})+w_{n}^{k+\frac{n}{2}}P_{o}(w_{n}^{2k+n}) =P_{e}(w_{n}^{2k})-w_{n}^{k}P_{o}(w_{n}^{2k}) $$

优化步骤 ③

步骤 ① 是已知系数，求 \(n-1\) 次多项式 \(P(x)\) 在 \(n\) 个 \(n\) 次单位根位置的值，可以看作矩阵相乘的形式。

$$ \left[\begin{matrix}P(w_{n}^{0}) \\P(w_{n}^{1}) \\P(w_{n}^{2}) \\\vdots \\P(w_{n}^{n-1})\end{matrix}\right]=\left[\begin{matrix}w_{n}^{0} & w_{n}^{0} & w_{n}^{0} & \cdots & w_{n}^{0} \\w_{n}^{0} & w_{n}^{1} & w_{n}^{2} & \cdots & w_{n}^{n-1} \\w_{n}^{0} & w_{n}^{2} & w_{n}^{4} & \cdots & w_{n}^{2(n-1)} \\\vdots & \vdots & \ddots & \vdots \\w_{n}^{0} & w_{n}^{n-1} & w_{n}^{2(n-1)} & \cdots & w_{n}^{(n-1)(n-1)}\end{matrix}\right]\left[\begin{matrix}p_{0} \\p_{1} \\p_{2} \\\vdots \\p_{n-1}\end{matrix}\right] $$

步骤 ③ 是已知 \(n\) 个点值，求多项式的系数，可以看作上述变换的逆变换。

$$ \left[\begin{matrix}p_{0} \\p_{1} \\p_{2} \\\vdots \\p_{n-1}\end{matrix}\right]=\left[\begin{matrix}w_{n}^{0} & w_{n}^{0} & w_{n}^{0} & \cdots & w_{n}^{0} \\w_{n}^{0} & w_{n}^{1} & w_{n}^{2} & \cdots & w_{n}^{n-1} \\w_{n}^{0} & w_{n}^{2} & w_{n}^{4} & \cdots & w_{n}^{2(n-1)} \\\vdots & \vdots & \ddots & \vdots \\w_{n}^{0} & w_{n}^{n-1} & w_{n}^{2(n-1)} & \cdots & w_{n}^{(n-1)(n-1)}\end{matrix}\right]^{-1}\left[\begin{matrix}P(w_{n}^{0}) \\P(w_{n}^{1}) \\P(w_{n}^{2}) \\\vdots \\P(w_{n}^{n-1})\end{matrix}\right] $$
$$ \left[\begin{matrix}w_{n}^{0} & w_{n}^{0} & w_{n}^{0} & \cdots & w_{n}^{0} \\w_{n}^{0} & w_{n}^{1} & w_{n}^{2} & \cdots & w_{n}^{n-1} \\w_{n}^{0} & w_{n}^{2} & w_{n}^{4} & \cdots & w_{n}^{2(n-1)} \\\vdots & \vdots & \ddots & \vdots \\w_{n}^{0} & w_{n}^{n-1} & w_{n}^{2(n-1)} & \cdots & w_{n}^{(n-1)(n-1)}\end{matrix}\right]^{-1}=\frac{1}{n}\left[\begin{matrix}w_{n}^{0} & w_{n}^{0} & w_{n}^{0} & \cdots & w_{n}^{0} \\w_{n}^{0} & w_{n}^{-1} & w_{n}^{-2} & \cdots & w_{n}^{-(n-1)} \\w_{n}^{0} & w_{n}^{-2} & w_{n}^{-4} & \cdots & w_{n}^{-2(n-1)} \\\vdots & \vdots & \ddots & \vdots \\w_{n}^{0} & w_{n}^{-(n-1)} & w_{n}^{-2(n-1)} & \cdots & w_{n}^{-(n-1)(n-1)}\end{matrix}\right] $$

如果将步骤 ① 表示为 \(FFT(w_{n},p_{0},p_{1},\cdots,p_{n-1})\)，则步骤 ③ 为 \(IFFT(w_{n},P(w_{n}^{0}),P(w_{n}^{1}),\cdots,P(w_{n}^{n-1}))=\frac{1}{n}FFT(w_{n}^{-1},P(w_{n}^{0}),P(w_{n}^{1}),\cdots,P(w_{n}^{n-1}))\)。

发表更新基础 / 模板17 分钟读完 (大约2511个字)

图论

本文内容参考《算法》，《算法导论》，OI Wiki。

拓扑排序

例题

实现

  • 时间复杂度为 \(O(n+m)\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
private static int[] topologicalSort(int n, int[][] edges) {
    int[] in = new int[n];
    List<Integer>[] g = new List[n];
    Arrays.setAll(g, k -> new ArrayList<>());
    for (var e : edges) {
        int u = e[0], v = e[1];
        g[u].add(v);
        in[v]++;
    }

    Queue<Integer> q = new ArrayDeque<>();
    for (int i = 0; i < n; i++) {
        if (in[i] == 0) {
            q.offer(i);
        }
    }

    int idx = 0;
    int[] res = new int[n];
    while (!q.isEmpty()) {
        int x = q.poll();
        res[idx++] = x;
        for (int y : g[x]) {
            if (--in[y] == 0) {
                q.offer(y);
            }
        }
    }

    // 拓扑排序不存在
    assert idx == n;

    return res;
}

最小生成树

例题

Prim

实现一：朴素版本

  • 时间复杂度为 \(O(n^{2})\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
private static int prim(int n, int[][] edges) {
    int[][] g = new int[n][n];
    for (int i = 0; i < n; i++) {
        Arrays.fill(g[i], Integer.MAX_VALUE);
        g[i][i] = 0;
    }
    for (var e : edges) {
        int u = e[0], v = e[1], w = e[2];
        if (g[u][v] > w) {
            g[u][v] = g[v][u] = w;
        }
    }

    int[] d = new int[n];
    Arrays.fill(d, Integer.MAX_VALUE);
    boolean[] vis = new boolean[n];

    int res = 0;
    d[0] = 0;
    for (int i = 0; i < n; i++) {
        int t = -1;
        for (int j = 0; j < n; j++) {
            if (!vis[j] && (t == -1 || d[t] > d[j])) {
                t = j;
            }
        }

        // 不是连通图，最小生成树不存在
        assert d[t] != Integer.MAX_VALUE;

        vis[t] = true;
        res += d[t];

        for (int j = 0; j < n; j++) {
            d[j] = Math.min(d[j], g[t][j]);
        }
    }

    return res;
}

实现二：优先队列优化

  • 时间复杂度为 \(O(m\log{m})\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
private static int prim(int n, int[][] edges) {
    List<int[]>[] g = new List[n];
    Arrays.setAll(g, k -> new ArrayList<>());
    for (var e : edges) {
        int u = e[0], v = e[1], w = e[2];
        g[u].add(new int[]{v, w});
        g[v].add(new int[]{u, w});
    }

    int[] d = new int[n];
    Arrays.fill(d, Integer.MAX_VALUE);
    boolean[] vis = new boolean[n];
    Queue<int[]> q = new PriorityQueue<>((a, b) -> a[1] - b[1]);

    int res = 0, cnt = 0;
    d[0] = 0;
    q.offer(new int[]{0, 0});
    while (!q.isEmpty()) {
        int u = q.poll()[0];
        if (vis[u]) continue;
        vis[u] = true;
        res += d[u];
        if (++cnt == n) break;
        for (int[] t : g[u]) {
            int v = t[0], w = t[1];
            if (!vis[v] && d[v] > w) {
                d[v] = w;
                q.offer(new int[]{v, d[v]});
            }
        }
    }

    // 不是连通图，最小生成树不存在
    assert cnt == n;

    return res;
}

Kruskal

  • 时间复杂度为 \(O(m\log{m})\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
private static int kruskal(int n, int[][] edges) {
    Arrays.sort(edges, (a, b) -> a[2] - b[2]);

    int cnt = 1, res = 0;
    UnionFind uf = new UnionFind(n);
    for (var e : edges) {
        int u = e[0], v = e[1], w = e[2];
        if (uf.connected(u, v)) continue;
        uf.union(u, v);
        res += w;
        if (++cnt == n) break;
    }

    // 不是连通图，最小生成树不存在
    assert cnt == n;

    return res;
}

最短路

例题

Dijkstra

  • 使用场景：解决边权非负的单源最短路问题。

实现一：朴素版本

  • 时间复杂度为 \(O(n^{2})\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
private static final int INF = (int) 1e9;

private static int dijkstra(int n, int[][] edges) {
    int[][] g = new int[n][n];
    for (int i = 0; i < n; i++) {
        Arrays.fill(g[i], INF);
        g[i][i] = 0;
    }
    for (var e : edges) {
        int u = e[0], v = e[1], w = e[2];
        g[u][v] = Math.min(g[u][v], w);
    }

    int[] d = new int[n];
    Arrays.fill(d, INF);
    boolean[] vis = new boolean[n];

    d[0] = 0;
    while (true) {
        int t = -1;
        for (int i = 0; i < n; i++) {
            if (!vis[i] && (t == -1 || d[t] > d[i])) {
                t = i;
            }
        }

        if (t == n - 1 || d[t] == INF) {
            break;
        }
        vis[t] = true;

        for (int i = 0; i < n; i++) {
            d[i] = Math.min(d[i], d[t] + g[t][i]);
        }
    }

    return d[n - 1] == INF ? -1 : d[n - 1];
}

实现二：优先队列优化

  • 时间复杂度为 \(O(m\log{m})\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
private static final int INF = (int) 1e9;

private static int dijkstra(int n, int[][] edges) {
    List<int[]>[] g = new List[n];
    Arrays.setAll(g, k -> new ArrayList<>());
    for (var e : edges) {
        int u = e[0], v = e[1], w = e[2];
        g[u].add(new int[]{v, w});
    }

    int[] d = new int[n];
    Arrays.fill(d, INF);
    boolean[] vis = new boolean[n];
    Queue<int[]> q = new PriorityQueue<>((a, b) -> a[1] - b[1]);

    d[0] = 0;
    q.offer(new int[]{0, 0});
    while (!q.isEmpty()) {
        int u = q.poll()[0];
        if (u == n - 1) break;
        if (vis[u]) continue;
        vis[u] = true;
        for (int[] t : g[u]) {
            int v = t[0], w = t[1];
            if (d[v] > d[u] + w) {
                d[v] = d[u] + w;
                q.offer(new int[]{v, d[v]});
            }
        }
    }

    return d[n - 1] == INF ? -1 : d[n - 1];
}

Bellman-Ford

  • 时间复杂度为 \(O(nm)\)。
  • 使用场景：解决任意边权的单源最短路问题；判断是否存在负环；解决有边数限制的单源最短路问题。

实现一：朴素版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
private static final int INF = (int) 1e9;

private static int bellmanFord(int n, int[][] edges) {
    int[] d = new int[n];
    Arrays.fill(d, INF);

    d[0] = 0;
    for (int i = 0; i < n; i++) {
        for (var e : edges) {
            int u = e[0], v = e[1], w = e[2];
            d[v] = Math.min(d[v], d[u] + w);
        }
    }

    // d[n - 1] == INF 时，最短路不存在
    return d[n - 1];
}

实现二：队列优化（不能存在负环）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
private static final int INF = (int) 1e9;

private static int spfa(int n, int[][] edges) {
    List<int[]>[] g = new List[n];
    Arrays.setAll(g, k -> new ArrayList<>());
    for (var e : edges) {
        int u = e[0], v = e[1], w = e[2];
        g[u].add(new int[]{v, w});
    }

    int[] d = new int[n];
    Arrays.fill(d, INF);
    Queue<Integer> q = new ArrayDeque<>();
    boolean[] on = new boolean[n];

    d[0] = 0;
    q.offer(0);
    on[0] = true;
    while (!q.isEmpty()) {
        int u = q.poll();
        on[u] = false;
        for (int[] t : g[u]) {
            int v = t[0], w = t[1];
            if (d[v] > d[u] + w) {
                d[v] = d[u] + w;
                if (!on[v]) {
                    q.offer(v);
                    on[v] = true;
                }
            }
        }
    }

    // d[n - 1] == INF 时，最短路不存在
    return d[n - 1];
}

Floyd-Warshall

  • 时间复杂度为 \(O(n^{3})\)。
  • 使用场景：解决任意边权的多源最短路问题。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
private static final int INF = (int) 1e9;

private static int[][] floyd(int n, int[][] edges) {
    int[][] dp = new int[n][n];
    for (int i = 0; i < n; i++) {
        Arrays.fill(dp[i], INF);
        dp[i][i] = 0;
    }
    for (var e : edges) {
        int u = e[0], v = e[1], w = e[2];
        dp[u][v] = Math.min(dp[u][v], w);
    }

    for (int k = 0; k < n; k++) {
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (dp[i][k] != INF && dp[k][j] != INF) {
                    dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j]);
                }
            }
        }
    }
    return dp;
}

最近公共祖先

例题

倍增

  • 预处理时间复杂度为 \(O(n\log{n})\)，查询时间复杂度为 \(O(\log{n})\)。
  • 原理：\(f[i][j]\) 表示节点 \(j\) 的第 \(2^{i}\) 个祖先，当利用倍增得到 \(f\) 时，对于任意两个节点 \(x,y\)，先将较深的节点向上跳到相同深度，然后两个节点贪心的向上跳到 \(\operatorname{lca}\) 下方距离它最近的节点，最后得到的节点就是 \(\operatorname{lca}\) 的直接子节点。（在进行倍增时，根节点的父节点可以是任何值，因为该值不会影响算法的正确性）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
private static void dfs(int x, int fa, List<Integer>[] g, int[][] f, int[] d) {
    f[0][x] = fa;
    for (int i = 1; 1 << i <= d[x]; i++) {
        f[i][x] = f[i - 1][f[i - 1][x]];
    }
    for (int y : g[x]) {
        if (y != fa) {
            d[y] = d[x] + 1;
            dfs(y, x, g, f, d);
        }
    }
}

private static int lca(int x, int y, int[][] f, int[] d) {
    if (d[x] > d[y]) {
        int t = x; x = y; y = t;
    }

    int diff = d[y] - d[x];
    for (int i = 0; i < 31; i++) {
        if ((diff >> i & 1) == 1) {
            y = f[i][y];
        }
    }

    if (x != y) {
        for (int i = 30; i >= 0; i--) {
            if (f[i][x] != f[i][y]) {
                x = f[i][x];
                y = f[i][y];
            }
        }
        x = f[0][x];
    }
    return x;
}

Tarjan

  • 离线查询算法，时间复杂度为 \(O((n+m)\log{n})\)。更精确的复杂度分析可以使用反阿克曼函数。
  • 原理：每当处理完一个子树，就将该子树的根节点和其父节点合并，特别注意合并的方向是 \(f[y]=x\)。然后我们会遍历包含当前节点 \(x\) 的查询，如果另一个节点 \(y\) 访问过，则 \(\operatorname{lca}(x,y)=\operatorname{find}(y)\)。至于为什么是这样，可以通过分类讨论得到。注意 \(q\) 需要像无向图一样，为单个查询存储双向边。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
private static void tarjan(int x, List<Integer>[] g, boolean[] vis, UnionFind uf, List<int[]>[] q, int[] ans) {
    vis[x] = true;
    for (int y : g[x]) {
        if (!vis[y]) {
            tarjan(y, g, vis, uf, q, ans);
            uf.union(x, y); // 注意 f[y] = x
        }
    }

    for (int[] t : q[x]) {
        int y = t[0], i = t[1];
        if (vis[y]) {
            ans[i] = uf.find(y);
        }
    }
}

树链剖分

  • 预处理时间复杂度为 \(O(n)\)，查询时间复杂度为 \(O(\log{n})\)。
  • 原理：将树划分为若干重链，树中的每条路径不会包含超过 \(\log{n}\) 条不同的重链，所以查询的时间复杂度为 \(O(\log{n})\)。第一次 DFS 得到每个节点的父节点，深度，以及根据子树大小得到每个节点的重子节点。第二次 DFS 通过优先遍历重子节点，再遍历轻子节点，从而得到每个节点所在重链的头节点。然后就可以进行查询，通过比较 \(x,y\) 所在重链的头节点，来向上跳跃，最终得到 \(\operatorname{lca}\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
private static void dfs1(int x, int fa, List<Integer>[] g, int[] f, int[] d, int[] s, int[] h) {
    f[x] = fa;
    s[x] = 1; h[x] = -1;
    for (int y : g[x]) {
        if (y != fa) {
            d[y] = d[x] + 1;
            dfs1(y, x, g, f, d, s, h);
            s[x] += s[y];
            if (h[x] == -1 || s[h[x]] < s[y]) {
                h[x] = y;
            }
        }
    }
}

private static void dfs2(int x, int head, List<Integer>[] g, int[] f, int[] h, int[] t) {
    t[x] = head;
    if (h[x] == -1) {
        return;
    }
    dfs2(h[x], head, g, f, h, t);
    for (int y : g[x]) {
        if (y != f[x] && y != h[x]) {
            dfs2(y, y, g, f, h, t);
        }
    }
}

private static int lca(int x, int y, int[] f, int[] d, int[] t) {
    while (t[x] != t[y]) {
        if (d[t[x]] > d[t[y]]) {
            x = f[t[x]];
        } else {
            y = f[t[y]];
        }
    }
    return d[x] < d[y] ? x : y;
}

强连通分量

例题

Tarjan

  • 时间复杂度为 \(O(n+m)\)。
  • 原理：\(dfn[x]\) 表示节点 \(x\) 的 DFS 编号；\(low[x]\) 表示节点 \(x\) 能够到达的节点的最小的 DFS 编号。我们将图看作一棵树，并定义四种边，那么强连通分量的根节点就是该分量中第一个被遍历到的节点，满足 \(dfn[x]=low[x]\)，所以，过程很复杂，难以描述，直接看 wiki 吧。（注意使用的时候，将 \(dfn\) 初始化为 \(-1\)，并且对所有节点调用该算法前，需要判断 \(dfn=-1\) 是否成立）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
private static int dfnCnt, sccCnt;

private static void tarjan(int x, List<Integer>[] g, int[] dfn, int[] low, Deque<Integer> stk, boolean[] on, int[] scc, int[] size) {
    dfn[x] = low[x] = dfnCnt++;
    stk.push(x);
    on[x] = true;

    for (int y : g[x]) {
        if (dfn[y] == -1) {
            tarjan(y, g, dfn, low, stk, on, scc, size);
            low[x] = Math.min(low[x], low[y]);
        } else if (on[y]) {
            low[x] = Math.min(low[x], dfn[y]);
        }
    }

    if (dfn[x] == low[x]) {
        for (int y = -1; y != x; ) {
            y = stk.pop();
            on[y] = false;
            scc[y] = sccCnt;
            size[sccCnt]++;
        }
        sccCnt++;
    }
}
关注我

链接

分类

最新文章

归档

标签

Debugging2
Draft1
Hexo1

链接

×