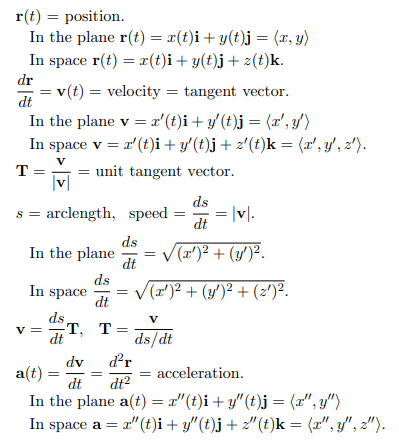Introduction to Linear Algebra
参考 Introduction to Linear Algebra,MIT 18.06SC Fall 2011,SOLUTIONS TO PROBLEM SETS。
Vectors and Matrices
Vectors and Linear Combinations
\(n\) 个 \(m\) 维向量组成 \(m \times n\) 矩阵 \(A\) 的列。两个关键问题:① 列向量的线性组合 \(Ax = x_{1}v_{1} + x_{2}v_{2} + \cdots + x_{n}v_{n}\) 是否填满整个空间?如果不能,则 \(A\) 是奇异矩阵,其列向量是线性相关的。② 已知 \(A\) 和 \(b\),求解 \(Ax = b\)。
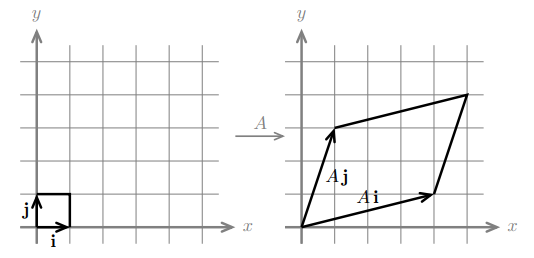
从列、行和矩阵角度理解:向量的线性组合,线性方程组,矩阵相乘。如果向量 \(v\) 和 \(w\) 线性无关(不共线),则 \(2 \times 2\) 矩阵 \(A=\left[\begin{matrix}v & w\end{matrix}\right]\) 是可逆的,向量 \(v\) 和 \(w\) 的线性组合可以填满 \(xy\) 平面。
Lengths and Angles from Dot Products
向量 \(v=\left[\begin{matrix}v_{1} \ v_{2} \ \vdots \ v_{n}\end{matrix}\right]\) 和 \(w=\left[\begin{matrix}w_{1} \ w_{2} \ \vdots \ w_{n}\end{matrix}\right]\) 的点积 \(v \cdot w = v_{1}w_{1} + v_{2}w_{2} + \cdots + v_{n}w_{n}\)。点积 \(v \cdot v\) 表示向量长度的平方 \(|v|^{2} = v_{1}^{2} + \cdots + v_{n}^{2}\)。单位向量 \(u\) 的长度 \(|u| = 1\),如果 \(v \neq 0\),则 \(u=\frac{v}{|v|}\) 是单位向量。
垂直向量满足 \(v \cdot w = 0\),则 \(|v + w|^{2} = |v|^{2} + |w|^{2}\)。如果 \(|v| = 1\) 且 \(|u| = 1\),则 \(v\) 和 \(u\) 之间的夹角 \(\theta\) 满足 \(\cos{\theta} = v \cdot u\)。如果 \(v\) 和 \(w\) 都不是零向量,则 \(\frac{v \cdot w}{|v||w|} = \cos{\theta}\)。SCHWARZ INEQUALITY \(|v \cdot w| \leq |v||w|\),TRIANGLE INEQUALITY \(|v + w| \leq |v| + |w|\)。
Matrices and Their Column Spaces
If I have numbers in \(A\) and \(x\), and I want to compute \(Ax\), then I tend to use dot products: the row picture. But if I want to understand \(Ax\), the column picture is better.
矩阵 \(A\) 的列向量线性无关意味着:① 只有 \(x\) 是零向量时,能使 \(Ax = 0\);② 每个列向量都不是之前列的线性组合,通常从左到右检查相关性。矩阵 \(A\) 的列向量的所有线性组合构成矩阵的列空间 \(C(A)\),或者说矩阵 \(A\) 的列向量张成(span)列空间。当且仅当 \(v\) 在矩阵 \(A\) 的列空间中,\(Ax = v\) 有解。对于 \(m \times m\) 矩阵 \(A\),所有列向量线性无关,才能张成整个 \(\mathbf{R}^{m}\) 空间,如果线性相关则只能张成得到 \(\mathbf{R}^{m}\) 的子空间。
Matrix Multiplication AB and CR
个人理解,矩阵相乘可以看作由向量点积组合而成,只不过将不同部分视为整体,就有不同的表现形式。例如,矩阵 \(A\)(\(m \times s\))乘以矩阵 \(B\)(\(s \times n\)):
① 矩阵 \(A\) 中的行向量点乘矩阵 \(B\) 中的列向量,得到矩阵 \(C\) 中的单个元素。
② 将矩阵 \(A\) 视为单个行向量,其每个分量都是一个列向量。该行向量点乘矩阵 \(B\) 中的列向量,则矩阵 \(C\) 中列向量是矩阵 \(A\) 中列向量的线性组合。
③ 将矩阵 \(B\) 视为单个列向量,其每个分量都是一个行向量。矩阵 \(A\) 中的行向量点乘该列向量,则矩阵 \(C\) 中行向量是矩阵 \(B\) 中行向量的线性组合。
④ 将矩阵 \(A\) 中的列向量和矩阵 \(B\) 中的行向量相乘(外积),得到秩为 \(1\) 的 \(m \times n\) 矩阵,将这些矩阵求和得到矩阵 \(C\)。
矩阵乘法不满足交换律 \(AB \neq BA\),但是满足结合率 \((AB)C = A(BC)\)。矩阵 \(A\) 右乘 \(B\) 得到 \(AB\),其列向量是 \(A\) 中列向量的线性组合(列变换);矩阵 \(A\) 左乘 \(B\) 得到 \(BA\),其行向量是 \(A\) 中行向量的线性组合(行变换)。
For computing by hand, I would use the row way to find each number in \(AB\). I visualize multiplication by columns: The columns \(Ab_{j}\) in \(AB\) are combinations of columns of \(A\).
矩阵的秩(rank)就是其线性无关的列向量的数目,所有秩为 \(r\) 的矩阵都可以表示为 \(r\) 个秩为 \(1\) 的矩阵之和。秩为 \(1\) 的 \(m \times n\) 矩阵的列空间是 \(m\) 维空间中的一条直线,其行空间是 \(n\) 维空间中的一条直线。
将矩阵 \(A\) 分解为 \(CR\),即 \(A = CR\),其中 \(C\) 由 \(A\) 中所有 \(r\) 个线性无关的列向量组成,\(r\) 就是矩阵 \(A\) 和 \(C\) 的秩。\(A\) 中列向量可以通过 \(C\) 中列向量的线性组合得到,而 \(R\) 中列向量表示如何组合可以得到 \(A\) 中对应的列向量。\(R\) 可以表示为 \(R=\left[\begin{matrix}I & F\end{matrix}\right]P\),其中 \(I\) 是单位矩阵,表示 \(A\) 中所有线性无关列如何由 \(C\) 中列向量组合得到,\(F\) 则表示线性相关列的组合方式,\(P\) 置换矩阵将列放在对应位置上。
\(A\) 中行向量的秩和列向量的秩相同,非正式证明:因为 \(R\) 包含 \(r \times r\) 单位矩阵 \(I\),所以 \(R\) 中所有 \(r\) 个行向量都是线性无关的,而 \(R\) 左乘 \(C\) 得到 \(A\),说明 \(A\) 中行向量是 \(R\) 中行向量的线性组合,那么 \(A\) 中行向量的秩也是 \(r\)。\(C\) 和 \(A\) 有相同的列空间,其列向量组是 \(A\) 列空间的一个基(basis)。\(R\) 和 \(A\) 有相同的行空间,其行向量组是 \(A\) 行空间的一个基。
Solving Linear Equations \(Ax = b\)

Elimination and Back Substitution
列向量线性无关的方阵 \(A\)(满秩矩阵),都可以被化简为主元(pivot)非零的上三角矩阵 \(U\)。如果主对角线上没有零,则上三角矩阵 \(U\) 满秩,所有列向量线性无关。将 \(A\) 转为 \(U\),相当于不断地左乘矩阵(消元矩阵 \(E\) 和 置换矩阵 \(P\))进行行变换。消元和置换过程可以使用增广矩阵 \(\left[\begin{matrix}A & b \end{matrix}\right]\),同时对 \(A\) 和 \(b\) 执行操作。
如果方阵 \(A\) 的列向量线性无关,则方程 \(Ax = b\) 有唯一解,因为 \(A\) 的列空间是整个 \(\mathbf{R}^{n}\)。否则,方程无解或有无穷多个解,取决于 \(b\) 是否在 \(A\) 的列空间中。如果 \(b\) 在 \(A\) 的列空间中,则存在 \(x\) 使得 \(Ax = b\)。而且 \(A\) 的列向量线性相关,所以 \(AX = 0\) 有无穷多个解,那么 \(A(x + \alpha X) = b\) 对任意 \(\alpha\) 都成立,所以此时方程有无穷多个解。
Elimination Matrices and Inverse Matrices
如果矩阵 \(A\) 是可逆的,则存在 \(A^{-1}\) 使得 \(AA^{-1} = A^{-1}A = I\)。矩阵 \(A\) 可逆当且仅当,消元之后所有主元非零,\(Ax = b\) 有唯一解 \(x = A^{-1}b\),\(Ax = 0\) 没有非零解,\(A\) 的列向量线性无关,\(A\) 的行列式 \(|A| \neq 0\),\(A\) 是非奇异矩阵。利用增广矩阵求逆矩阵,将 \(\left[\begin{matrix}A & I \end{matrix}\right]\) 转化为 \(\left[\begin{matrix}I & A^{-1} \end{matrix}\right]\)。
\(B^{-1}A^{-1}\) illustrates a basic rule of mathematics: Inverses come in reverse order. It is also common sense: If you put on socks and then shoes, the first to be taken off are the shoes.
矩阵乘积的逆满足 \(ABB^{-1}A^{-1} = I \Rightarrow (AB)^{-1} = B^{-1}A^{-1}\),逆变换以相反的顺序执行。任意可逆矩阵都可以分解为 \(LU\) 的形式,\(EPA = U \Rightarrow PA = E^{-1}U = LU\),\(L\) 和 \(U\) 分别是下三角矩阵和上三角矩阵。假设 \(n = 3\),且置换矩阵 \(P = I\)。\(E_{ij}\) 表示 \(row_{i} = row_{i} - l_{ij} \times row_{j}\) 行变换,不断执行行变换消元,得到消元矩阵 \(E = E_{32}E_{31}E_{21}\)。其逆矩阵为 \(E^{-1} = E_{32}^{-1}E_{31}^{-1}E_{21}^{-1}\),所有的乘数 \(l_{ij}\) 都在矩阵 \(L\) 的相应位置上。
Matrix Computations and \(A = LU\)
The elimination steps from A to U cost \(\frac{1}{3}n^{3}\) multiplications and \(\frac{1}{3}n^{3}\) subtractions.
Each right side \(b\) costs only \(n^{2}\): forward to \(Ux = c\), then back-substitution for \(x\).
什么时候可以将矩阵 \(A\) 分解为 \(LU\),而不需要交换行(\(P = I\)),且所有主元非零?矩阵 \(A\) 的所有左上角的 \(k \times k\) 子矩阵必须是可逆的,其中 \(k \in [1, n]\)。因为消元也会分解每个 \(k \times k\) 子矩阵 \(A_{k}\),从 \(A = LU\) 得到 \(A_{k} = L_{k}U_{k}\),所以 \(A_{k}\) 必须是可逆的。
Permutations and Transposes
置换矩阵 \(P\) 和单位矩阵 \(I\) 有相同的行,只不过可以任意排列,总共有 \(n!\) 种排列方式。置换矩阵的性质:\(P^{T} = P^{-1}\);\(P\) 的列向量是正交的,列向量之间的点积都是零;置换矩阵的乘积 \(P_{1}P_{2}\) 也是置换矩阵;如果矩阵 \(A\) 可逆,则存在置换矩阵 \(P\),使得对 \(PA\) 消元可以得到主元非零的矩阵 \(U\),即 \(PA = LU\) 分解。可以在 \(A\) 中添加特殊的 \(1\ 2\ 3\) 列,该列跟踪原始的行号,可以从中得到 \(P\) 的值。
转置矩阵 \(A^{T}\) 的列和矩阵 \(A\) 的行相对应,相当于沿主对角线翻转矩阵 \(A\),满足 \((A^{T})_{ij} = A_{ji}\)。转置矩阵的性质:\((A + B)^{T} = A^{T} + B^{T}\),\((AB)^{T} = B^{T}A^{T}\),\((A^{-1})^{T} = (A^{T})^{-1}\)。
\(n \times 1\) 的列向量 \(x\) 和 \(y\) 的点积(内积)相当于 \(x^{T}y\),得到 \((1 \times n)(n \times 1) = 1 \times 1\) 矩阵;而外积相当于 \(xy^{T}\),得到 \((n \times 1)(1 \times n) = n \times n\) 矩阵。\(A^{T}\) 满足 \((Ax)^{T}y = x^{T}(A^{T}y)\),即 \(Ax\) 和 \(y\) 的内积等于 \(x\) 和 \(A^{T}y\) 的内积。
对称矩阵 \(S\) 满足 \(S^{T} = S\),即 \(s_{ji} = s_{ij}\)(反对称矩阵满足 \(S^{T} = -S\))。如果对称矩阵 \(S\) 是可逆的,则 \(S^{-1}\) 也是对称矩阵,因为 \((S^{-1})^{T} = (S^{T})^{-1} = S^{-1}\)。对于任意矩阵 \(A\),\(AA^{T}\) 是对称矩阵,因为 \((AA^{T})^{T} = (A^{T})^{T}A^{T} = AA^{T}\)。
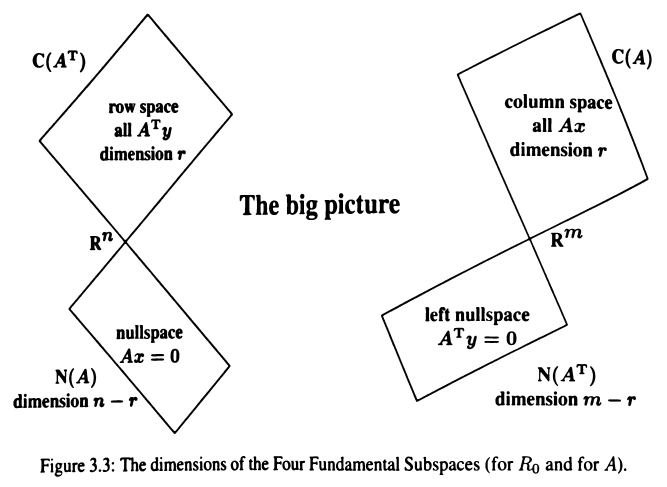
The Four Fundamental Subspaces
Vector Spaces and Subspaces
向量空间的定义,向量加法 \(x + y\) 和标量乘法 \(cx\) 必须满足以下八个规则。向量空间的子空间是满足以下条件的向量集合:如果 \(v\) 和 \(w\) 在子空间中,且 \(c\) 和 \(d\) 是任意标量,则所有线性组合 \(cv + dw\) 都在子空间中。矩阵 \(A\) 的列向量的所有线性组合构成列空间 \(C(A)\),方程 \(Ax = b\) 有解当且仅当 \(b\) 在 \(A\) 的列空间中,因为 \(b\) 是 \(A\) 的列向量的线性组合。矩阵 \(A\) 的行是 \(A^{T}\) 的列,所以 \(A\) 的行空间就是 \(A^{T}\) 的列空间 \(C(A^{T})\)。

Computing the Nullspace by Elimination: \(A=CR\)
将 \(Ax = 0\) 化简为阶梯形式 \(Rx = 0\),如果 \(A\) 可逆,则 \(R = I\),否则 \(R=\left[\begin{matrix}I & F\end{matrix}\right]P\)。公式 \(H = WF\) 中,\(W\) 表示 \(A\) 中线性无关的列向量,\(H\) 表示 \(A\) 中线性相关的列向量,\(F\) 表示如何组合 \(A\) 中线性无关的列向量,可以得到 \(A\) 中线性相关的列向量。\(P\) 置换矩阵表示将线性无关的列向量放在 \(A\) 的对应位置上。行最简形矩阵 \(R\) 中,矩阵每行第一个非零元素被称为主元,主元所在的列是主元列,其余列是自由列,主元列对应的变量是主元变量,自由列对应的变量是自由变量。
\(R_{0}\) 是包含零行的 \(R\) 的变体 \(R_{0} = \left[\begin{matrix}I & F \ 0 & 0\end{matrix}\right]P\),\(R_{0}\) 中 \(I\) 的位置指示 \(A\) 中线性无关列向量的位置,从而可以将 \(A = CR\) 中的 \(C\) 求出。\(C\) 的列向量和 \(R\) 的行向量分别张成 \(A\) 的列空间和行空间,它们分别是列空间和行空间的一个基。
矩阵 \(A\) 的零空间 \(N(A)\) 由 \(Ax = 0\) 的所有解组成。当矩阵 \(A\) 是可逆矩阵时,\(A\) 的列向量线性无关,\(Ax = 0\) 只有零解 \(x = 0\),此时零空间只包含零向量。否则,当 \(m \times n\) 矩阵 \(A\) 有 \(r\) 个线性无关的列时,\(Ax = 0\) 有 \(n - r\) 个特殊解(special solutions),这些特殊解是零空间的一个基,它们的线性组合是 \(Ax = 0\) 的通解,可以直接使用以下方法求出。
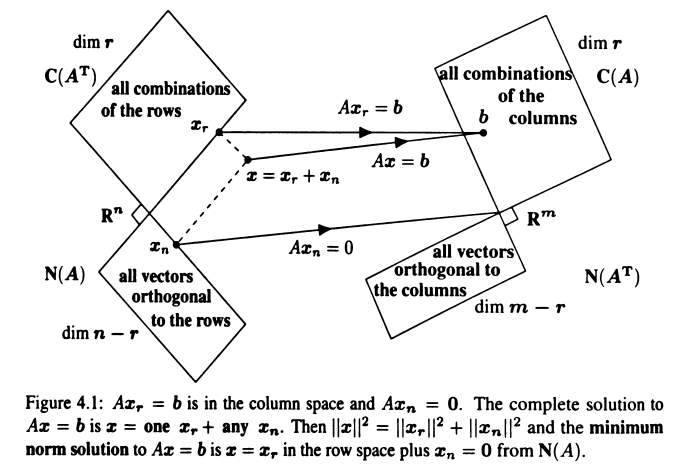
The Complete Solution to \(Ax = b\)
将 \(Ax = b\) 化简为 \(R_{0}x = d\),可以利用增广矩阵 \(\left[\begin{matrix}A & b\end{matrix}\right]\) 消元得到 \(\left[\begin{matrix}R_{0} & d\end{matrix}\right]\)。要使 \(Ax = b\) 有解,则 \(R_{0}\) 中的零行在 \(d\) 中也必须是零,此时 \(b\) 在 \(A\) 的列空间中。自由变量 \(x_{2} = x_{4} = 0\) 取值为零,可以得到主元变量 \(x_{1} = 1\) 和 \(x_{3} = 6\),此时得到 \(Ax = b\) 的特定解(particular solution)为 \(x_{p} = (1, 0, 6, 0)\)。当自由变量取零时,因为主元列组成单位矩阵,所以特定解中主元变量的值和 \(d\) 中的值相对应。\(Ax = b\) 的完整解(complete solution )由特定解 \(x_{p}\) 和零空间中的向量 \(x_{n}\) 组成。
对于 \(m \times n\) 矩阵,有 \(r \leq \min(m, n)\)。如果矩阵是方阵且满秩(\(r = m = n\)),则方程组有唯一解;如果矩阵不是方阵且列满秩(\(r = n < m\)),则方程组无解或者有唯一解;如果矩阵不是方阵且行满秩(\(r = m < n\)),则方程组有无穷多个解;如果矩阵不满秩(\(r < m, r < n\)),则方程组无解或者有无穷多个解。
Independence, Basis, and Dimension
如果 \(Ax = 0\) 只有零解 \(x = 0\),即零空间 \(N(A)\) 中只有零向量,则矩阵 \(A\) 的列向量线性无关。如果矩阵 \(A\) 是列满秩的,则 \(A\) 的列向量线性无关,此时矩阵 \(A\) 有 \(n\) 个主元、没有自由变量、\(A = CR\) 分解中 \(R = I\)、零空间中只有零向量。如果 \(m \times n\) 矩阵 \(A\) 有 \(n > m\),则矩阵 \(A\) 的列向量必定线性相关,矩阵 \(A\) 的秩 \(r \leq m < n\)、至多有 \(m\) 个主元、\(Ax = 0\) 有 \(n - m\) 个自由变量、\(Ax = 0\) 有非零解。
Another way to describe linear dependence is this: “One vector is a combination of the other vectors.” That sounds clear. Why don’t we say this from the start? Our definition was longer: “Some combination gives the zero vector, other than the trivial combination with every \(x = 0\).” We must rule out the easy way to get the zero vector.
向量空间的基是线性无关的一组向量,它们张成该向量空间。向量空间中的任意向量 \(v\),对应基向量的唯一线性组合。\(n \times n\) 单位矩阵的列向量,构成 \(\mathbf{R}^{n}\) 的标准基。每个 \(n \times n\) 可逆矩阵的列向量组,都构成 \(\mathbf{R}^{n}\) 的一个基。向量空间的基总是包含相同数量的向量,基向量的数量是该向量空间的维数。矩阵列空间的维数等于矩阵的秩。
零向量永远不会作为基向量,因为零向量总是和其他向量线性相关。将零向量的系数设为任意非零值,其他向量的系数设为零,就可以得到 \(Ax = 0\) 的非零解。只包含零向量的空间 \(\mathbf{Z}\) 的维数是零,空集是该空间的基。
Dimensions of the Four Subspaces
\(A\) 的行空间是 \(A^{T}\) 的列空间,\(A\) 的左零空间是 \(A^{T}\) 的零空间。之所以称为左零空间,是因为该空间由 \(xA = 0\) 的所有解组成,\(xA = 0 \rightarrow A^{T}x^{T} = 0 \rightarrow A^{T}y = 0\)。行变换不会改变行空间和零空间(变换矩阵是可逆的),但是会改变列空间和左零空间,列变换同理。列空间的基是 \(R\) 的 \(r\) 个主元列在 \(A\) 中对应的列,行空间的基是 \(R\) 的 \(r\) 个行,零空间的基是 \(Rx = 0\) 的 \(r\) 个特解。如果 \(EA = R_{0}\),因为 \(R_{0}\) 的最后 \(m - r\) 行都是零,所以左零空间的基是 \(E\) 的最后 \(m - r\) 行。消元矩阵 \(E\) 可以通过将增广矩阵 \(\left[\begin{matrix}A & I\end{matrix}\right]\) 消元为 \(\left[\begin{matrix}R_{0} & E\end{matrix}\right]\) 得到。

矩阵 \(AB\) 的行是矩阵 \(B\) 的行的线性组合,所以 \(rank(AB) \leq rank(B)\)。矩阵 \(AB\) 的列是矩阵 \(A\) 的列的线性组合,所以 \(rank(AB) \leq rank(A)\)。也就是说,\(rank(AB) \leq \min(rank(A), rank(B))\)。当矩阵 \(B\) 可逆时,\(rank(AB) = rank(A)\)。以下是推导过程,假设 \(A\) 是 \(m \times n\) 矩阵,\(B\) 是 \(n \times n\) 矩阵。
Orthogonality
Orthogonality of Vectors and Subspaces
正交向量满足 \(v \cdot w = v^{T}w = 0\) 和 \(|v|^{2} + |w|^{2} = |v + w|^{2}\)。如果子空间 \(V\) 中的任意向量 \(v\) 和子空间 \(W\) 中的任意向量 \(w\) 满足 \(v^{T}w = 0\),则子空间 \(V\) 和 \(W\) 正交。如果 \(V\) 和 \(W\) 是 \(\mathbf{R}^{n}\) 中的正交子空间,则 \(\dim{V} + \dim{W} \leq n\)。\(V\) 的正交补 \(V^{\perp}\) 包含所有和 \(V\) 正交的向量。两个正交子空间的交集仅包含零向量。每个秩为 \(r\) 的矩阵都有 \(r \times r\) 的可逆子矩阵。
任意矩阵 \(A\) 的行空间和零空间正交,列空间和左零空间正交。非正式证明:零空间的向量 \(x\) 满足 \(Ax = 0\),可以发现 \(A\) 中的每个行向量点乘 \(x\) 都是零,所以 \(A\) 中行向量的线性组合和 \(x\) 正交,即行空间和零空间正交。正式证明:假设 \(x\) 在零空间中、\(A^{T}y\) 在行空间中,则 \(x\) 满足 \(Ax = 0\),两者的内积 \(x^{T}(A^{T}y) = (Ax)^{T}y = 0^{T}y = 0\),所以零空间和行空间正交。同理,可以证明列空间和左零空间正交。
行空间和零空间互为正交补 \(r + (n - r) = n\),列空间和左零空间互为正交补 \(r + m - r = m\)。行空间和零空间组合构成整个 \(\mathbf{R}^{n}\) 空间,列空间和左零空间组合构成整个 \(\mathbf{R}^{m}\) 空间。\(\mathbf{R}^{n}\) 空间中的向量可以表示为 \(x = x_{row} + x_{null}\),\(\mathbf{R}^{m}\) 中的向量可以表示为 \(y = y_{col} + y_{null}\)。对于 \(Ax = b, x = x_{r} + x_{n}\),列空间中的每个向量 \(b\) 都由行空间中唯一的向量 \(x_{r}\) 确定。
Projections onto Lines and Subspaces
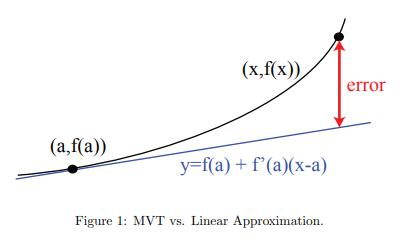
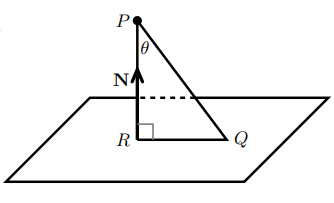
假设向量 \(b\) 在向量 \(a\) 所在直线上的投影是向量 \(p\),则向量 \(p\) 是向量 \(a\) 的倍数,误差向量(error vector)\(e = b - p\) 和向量 \(a\) 垂直。如果 \(b = a\),投影 \(p = a\)。如果 \(a^{T}b = 0\),则投影 \(p = 0\)。向量 \(bpe\) 组成直角三角形的三条边。
将向量 \(b\) 投影到向量 \(a\) 所在直线上的投影矩阵 \(P\) 满足 \(p = Pb\) 和 \(P^{2} = P = P^{T}\)。通过以下推导可知,矩阵 \(P\) 由列向量 \(a\) 和行向量 \(a^{T}\) 的外积再除以 \(a^{T}{a}\) 得到,它的秩为 \(1\),而且和向量 \(b\) 无关,只和向量 \(a\) 有关。如果 \(P\) 将向量投影到某个子空间,则 \(I - P\) 将向量投影到该子空间的正交子空间中。
将向量 \(b\) 投影到 \(m \times n\) 列满秩矩阵 \(A\) 的列空间中,投影向量 \(p\) 根据矩阵 \(A\) 列向量的某种组合 \(\hat{x}\) 得到,误差向量 \(e = b - p\) 和 \(A\) 的列空间垂直,\(|e|\) 是向量 \(b\) 到列空间的距离。根据垂直关系,分别求解得到向量 \(\hat{x}\)、投影向量 \(p\) 以及投影矩阵 \(P\)。对称矩阵 \(A^{T}A\) 是可逆的,当且仅当 \(A\) 的列向量线性无关,两者有相同的零空间 \(\mathbf{N}(A^{T}A) = \mathbf{N}(A)\)。如果 \(P\) 是可逆矩阵,则必然有 \(P^{-1}P^{2} = P^{-1}P \rightarrow P = I\)。
Least Squares Approximations
假设矩阵 \(A\) 的列向量线性无关,误差 \(e = b - Ax\) 不总是为零,当 \(e\) 为零时,\(x\) 是 \(Ax = b\) 的精确解。否则,假设 \(e\) 的长度在 \(\hat{x}\) 处取到最小值 \(|b - A\hat{x}|^{2}\),此时 \(\hat{x}\) 是 \(Ax = b\) 的最小二乘解。误差 \(e\) 何时取到最小值?
几何角度:当 \(b\) 不在 \(Ax\) 的列空间中时,找到列空间中最接近 \(b\) 的点 \(p\),该 \(p\) 就是 \(b\) 在列空间上的投影,此时 \(e\) 的长度最小,根据上节投影知识,知道 \(\hat{x}\) 满足 \(A^{T}A\hat{x} = A^{T}b\)。代数角度:将向量 \(b\) 分解为在 \(Ax\) 的列空间中的向量 \(p\) 和垂直列空间的向量 \(e\),\(Ax = b = p + e\) 无解,但是 \(Ax = p\) 有解,误差向量长度的平方 \(|Ax - b|^{2} = |Ax - p|^{2} + |e|^{2}\),当 \(Ax = p\) 时误差最小,此时 \(x = \hat{x}\)。(还有微积分角度,偏导为零)
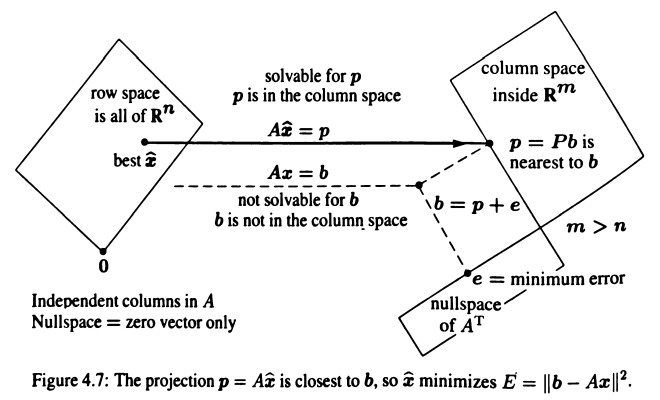
如果矩阵 \(A\) 的列向量线性相关,此时 \(A^{T}A\) 不可逆,不能使用 \(A^{T}A\hat{x} = A^{T}b\) 求解 \(\hat{x}\)。将 \(b\) 分解为 \(b = p + e\),此时 \(A\hat{x} = p\) 有无穷多个解,因为 \(A\) 的零空间有非零向量。
Orthonormal Bases and Gram-Schmidt
互相垂直的单位向量(长度为 \(1\) 的向量)构成的基被称为标准正交基(orthonormal basis)。注意,标准基(standard basis)是标准正交基的特例。如果 \(m \times n\) 矩阵 \(Q\) 的列向量是标准正交的,则 \(Q^{T}Q = I\)。如果 \(Q\) 不是方阵,则反过来不成立 \(QQ^{T} \neq I\)。如果 \(Q\) 是方阵,则 \(Q^{T}Q = I\) 意味着 \(Q^{T} = Q^{-1}\),此时 \(Q\) 被称为正交矩阵。每个置换矩阵都是正交矩阵。如果 \(Q\) 的列向量是标准正交的,则 \((Qx)^{T}(Qy) = x^{T}Q^{T}Qy = x^{T}y\),所以 \(|Qx| = |x|\)。
如果投影使用列向量标准正交的矩阵 \(Q\),而不是列向量线性无关的矩阵 \(A\),可以得到如下公式。投影 \(p\) 由标准正交向量组合而成,其分量是 \(q_{i}(q_{i}^{T}b) = q_{i}(|q_{i}||b|\cos{\theta_{i}}) = q_{i}(|b|\cos{\theta_{i}})\)。
使用 Gram-Schmidt 方法,从线性无关向量 \(a_{1},\cdots,a_{n}\) 构造标准正交向量 \(q_{1},\cdots,q_{n}\)。首先将 \(a_{1}\) 作为第一个正交向量 \(A_{1}\),假设当前已经处理到 \(a_{j}\),之前的标准正交向量是 \(q_{1}\) 到 \(q_{j - 1}\)。那么第 \(j\) 个正交向量 \(A_{j}\) 就是 \(a_{j}\) 中和之前所有正交向量都垂直的分量,求该分量类似求投影中的误差向量 \(e\)。让 \(a_j\) 减去其在所有 \(q_{i}\) 上的投影向量 \(p_{j}\),得到的就是分量 \(A_{j}\),再除以自身长度就得到标准正交向量 \(q_{j}\)。
使用该方法构造的向量满足 \(A = QR\),矩阵 \(R = Q^{T}A\) 是上三角矩阵,因为之后的 \(q\) 和之前的 \(a\) 正交。因为 \(A\) 的列向量线性无关,\(a_{i}\) 在 \(q_{i}\) 上的分量必然不为零,所以 \(R\) 中的对角元素都是非零正数,矩阵 \(R\) 可逆。正交矩阵 \(Q_{1}\) 乘以正交矩阵 \(Q_{2}\) 结果仍是正交矩阵,\(Q_{2}^{T}Q_{1}^{T}Q_{1}Q_{2} = I = (Q_{1}Q_{2})^{T}(Q_{1}Q_{2})\)。
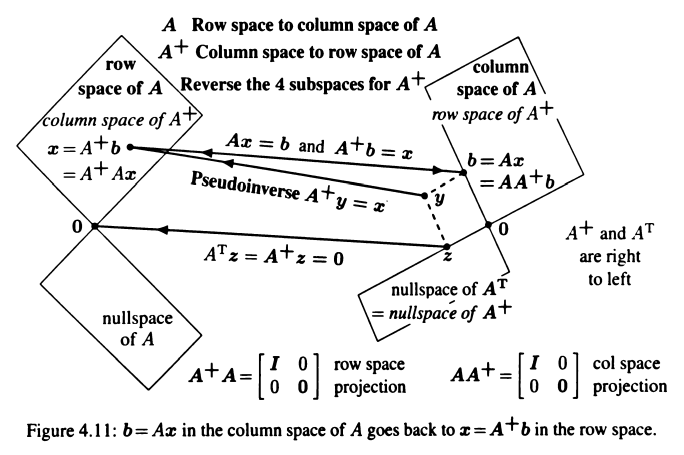
The Pseudoinverse of a Matrix
每个矩阵 \(A\) 都有伪逆 \(A^{+}\)。当 \(r = n < m\) 时,\(Ax = b\) 无解或者有唯一解,左逆 \(A^{+}\) 对应方程的最小二乘解 \(\hat{x} = (A^{T}A)^{-1}A^{T}b = A^{+}b\)。当 \(r = m < n\) 时,\(Ax = b\) 有无穷多个解,右逆 \(A^{+}\) 对应方程的最小长度解 \(x^{+} = A^{+}b\),通解是 \(x = x^{+} + x_{n}\),最小长度意味着在零空间中的分量为零。当 \(r < m, n\) 时,\(Ax = b\) 无解或者有无穷多个解,伪逆 \(A^{+}\) 对应方程的最小范数(norm)最小二乘解 \(x^{+} = A^{+}b\),不仅最小化 \(|Ax - b|^{2}\),而且最小化 \(|x|\)。

对于 \(m \times n\) 矩阵 \(A\),其伪逆 \(A^{+}\) 是 \(n \times m\) 矩阵。每个在 \(m\) 维空间中的向量 \(y\) 可以分解为垂直的两部分 \(y = b + z\),\(b\) 在 \(A\) 的列空间中,\(z\) 在 \(A\) 的左零空间中,行空间中的某个向量 \(x\) 满足 \(Ax = b\)。\(A^{+}\) 和 \(A^{T}\) 有相同的四个子空间,\(A^{+}A\) 将向量投影到矩阵 \(A\) 的行空间中,\(AA^{+}\) 将向量投影到矩阵 \(A\) 的列空间中。
Determinants
3 by 3 Determinants and Cofactors
单位矩阵的行列式有 \(\det{I} = 1\),行交换会反转行列式的符号,行向量乘以某个数会使行列式也乘以该数,行列式是行向量的多重线性函数,\(n\) 阶行列式有 \(n!\) 项,每项包含不同行不同列的元素。矩阵 \(A\) 中元素 \(a_{ij}\) 的余子式(minor)\(M_{ij}\) 是将第 \(i\) 行第 \(j\) 列移除之后,剩余的 \(n - 1\) 阶子矩阵的行列式。元素 \(a_{ij}\) 的代数余子式(cofactor)\(C_{ij}\) 是余子式乘以符号因子 \(C_{ij} = (-1)^{i + j}M_{ij}\)。将第 \(i\) 行中的元素分别乘以对应的代数余子式,然后求和可以得到矩阵 \(A\) 的行列式。
将矩阵 \(A\) 乘以对应的代数余子式矩阵 \(C\) 的转置(伴随矩阵),将会得到 \((\det{A})I\)。对角线以外的元素都为零,因为其余元素都可以看作是具有两个相同行的矩阵的行列式,行交换会改变行列式的符号,而交换两个相同行得到的行列式相同,所以该矩阵的行列式是零,即其余元素的值为零。由于 \(A^{-1}\) 需要除以行列式得到,所以可逆矩阵的行列式不等于零。逆矩阵 \(A^{-1}\) 中的每个元素,都由两个行列式之比得到(代数余子式比 \(A\) 的行列式)。
Computing and Using Determinants
三角矩阵和对角矩阵的行列式可以由对角线元素相乘得到,转置矩阵和原矩阵的行列式相同,矩阵乘积的行列式等于矩阵行列式的乘积。矩阵相加的行列式不意味着矩阵行列式相加,例如 \(\det{I + I} = 2^{n}\)。正交矩阵的行列式为 \(\pm{1}\),可逆矩阵的行列式为主元乘积再乘上 \(\pm{1}\),矩阵 \(U\) 的行列式是主元乘积,矩阵 \(L\) 的行列式是 \(1\),矩阵 \(P\) 的行列式是 \(\pm{1}\)。
克莱姆法则:如果 \(\det{A}\) 不为零,则可以使用行列式求解 \(Ax = b\),矩阵 \(B_{j}\) 通过将 \(A\) 的第 \(j\) 列替换为向量 \(b\) 得到。
Eigenvalues and Eigenvectors
Introduction to Eigenvalues: \(Ax = \lambda x \)
对于 \(n \times n \) 矩阵 \(A \),如果存在非零向量 \(x \) 和标量 \(\lambda \) 使得 \(Ax = \lambda x \),则 \(x \) 和 \(\lambda \) 分别是矩阵 \(A \) 的特征向量和特征值。特征向量 \(x \) 乘矩阵 \(A \) 不会改变方向,只是变为原来的 \(\lambda \) 倍。矩阵 \(A \) 存在特征向量的前提是,\((A - \lambda I)x = 0 \) 有非零解,所以有 \(\det{(A - \lambda I)} = 0 \)。求解该方程可以得到 \(n \) 个特征值(可能重复),然后代入 \((A - \lambda I)x = 0 \) 求解特征向量,特征向量 \(x \) 在矩阵 \(A - \lambda I \) 的零空间中。矩阵 \(A \) 的特征向量 \(x \) 也是矩阵 \(A^{n} \) 的特征向量,只是特征值变为 \(\lambda^{n} \),有 \(A^{n}x = \lambda^{n}x \)。
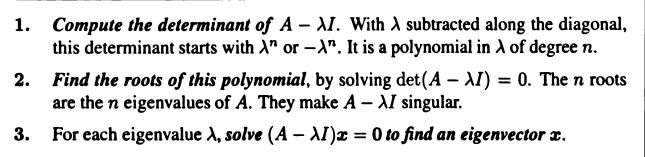
对于投影矩阵 \(P \),其列空间中的向量 \(x \) 投影到自身 \(Px = x \),其零空间中的向量 \(x \) 投影到零 \(Px = 0x \)。有特征值 \(\lambda = 0 \) 和 \(\lambda = 1 \),特征向量 \(x_{1} = (1, 1) \) 和 \(x_{2} = (1, -1) \)。矩阵 \(P \) 是 Markov 矩阵,每列之和为 \(1 \),必然有特征向量 \(\lambda = 1 \)。矩阵 \(P \) 是奇异矩阵,因为有特征值 \(\lambda = 0 \),所以有 \(\det{(A - \lambda I)} = \det{A} = 0 \)。矩阵 \(P \) 是对称矩阵,特征向量必然正交。如果矩阵偏移单位向量 \(I \),则特征值偏移 \(1 \),特征向量不变,因为 \((A + I)x = (\lambda + 1)x \)。
矩阵 \(A \) 的特征值的乘积等于其行列式,特征值之和等于其主对角线元素和(\(A \) 的迹,trace)。三角矩阵 \(U \) 的特征值就是其主对角线上的元素,因为 \(\det{(A - \lambda I)} \) 就是其主对角线上的元素之积。消元不会改变行列式,但是会改变特征值。正交矩阵 \(Q \) 的特征值的绝对值满足 \(|\lambda| = 1 \),因为 \(|Qx| = |x| \rightarrow |\lambda x| = |x| \)。对称矩阵的特征值为实数,反对称矩阵的特征值为纯虚数。如果矩阵 \(A \) 的特征值是 \(\lambda \),矩阵 \(B \) 的特征值是 \(\beta \),且 \(x \) 是 \(A \) 和 \(B \) 的特征向量,则 \(ABx = A\beta x = \beta Ax = \beta \lambda x \)。
Diagonalizing a Matrix
如果 \(n \times n \) 矩阵 \(A \) 有 \(n \) 个线性无关的特征向量 \(x_{1},\dots,x_{n} \),将这些特征向量作为矩阵 \(X \) 的列向量,则 \(X^{-1}AX \) 是特征值对角矩阵 \(\Lambda \),此时矩阵 \(A \) 被对角化。\(A^{k} \) 有相同的特征向量矩阵 \(X \),特征值对角矩阵 \(\Lambda \) 变为 \(\Lambda^{k} \)。如果矩阵 \(A \) 有 \(n \) 个不同的特征值,则其必然有 \(n \) 个线性无关的特征向量,矩阵可以被对角化。可逆和可对角化之间没有关系,可逆意味着特征值不为零,可对角化意味着有 \(n \) 个线性无关的特征向量。
所有矩阵 \(A = BCB^{-1} \) 是相似的(similar),它们有和矩阵 \(C \) 相同的特征值,矩阵 \(B \) 是任意可逆矩阵。如果 A 是 \(m \times n \) 矩阵,\(B \) 是 \(n \times m \) 矩阵,\(AB \) 和 \(BA \) 有相同的非零特征值。可以利用特征向量的性质求斐波那契数列的第 \(k \) 项。