参考 Reducible。
问题
如何求两个 \(n\) 次多项式 \(A(x)\) 和 \(B(x)\) 的乘积 \(C(x)\)?最简单的方式是使用乘法分配律对每个系数做乘积,时间复杂度为 \(O(n^{2})\)。
另一种想法是:① 在多项式 \(A(x)\) 和 \(B(x)\) 上取 \(2n+1\) 个点 \(x_{i}\),其中 \(i=0,1,\cdots,2n\),求出对应的函数值。② 根据 \(C({x_{i}})=A(x_{i})\cdot B(x_{i})\),可以得到 \(C(x)\) 上的 \(2n+1\) 个点。③ 使用拉格朗日插值,化简得到 \(C(x)\) 的表达式。总时间复杂度为 \(O(n^{2})\),如果能够将 ① 和 ③ 的时间复杂度优化为 \(O(n\log{n})\),那么就能够降低总时间复杂度。
优化步骤 ①
可以发现,对于偶函数 \(f(x)=f(-x)\),对于奇函数 \(f(x)=-f(-x)\)。如果将多项式分解为偶函数和奇函数两部分,则可以可以利用对称性快速求点值。不妨设 \(n\) 为偶数,将 \(n-1\) 次多项式 \(P(x)\) 划分为偶函数和奇函数两部分。
设 \(P_{e}(x)=p_{0}+p_{2}x^{1}+\cdots+p_{n-2}x^{\frac{n}{2}-2}\),\(P_{o}(x)=p_{1}+p_{3}x^{2}+\cdots+p_{n-1}x^{\frac{n}{2}-2}\),则 \(P(x)=P_{e}(x^{2})+xP_{o}(x^{2})\)。此时,如果取 \(n\) 个点 \(\pm x_{0},\pm x_{1},\cdots,\pm x_{\frac{n}{2}-1}\),则只需要计算 \(P_{e}(x_{i}^{2})\) 和 \(P_{o}(x_{i}^{2})\),就能够通过以下方式得到两个函数值。
所以,要求 \(P(x)\) 上的 \(n\) 个点值,等价于求 \(P_{e}(x^{2})\) 和 \(P_{o}(x^{2})\) 上的 \(\frac{n}{2}\) 个点值,即点 \(x_{0},x_{1},\cdots,x_{\frac{n}{2}-1}\) 的值。此时,原问题被分解为两个相同的子问题,并且子问题的大小只有原问题的一半,如果子问题能够按照原问题的方式继续分解,则可以得到时间复杂度为 \(O(n\log{n})\) 的算法。
但是,\(P_{e}(x^{2})\) 和 \(P_{o}(x^{2})\) 不能继续分解,因为定义域 \(x^{2}\geq 0\),点 \(x_{0}^{2},x_{1}^{2},\cdots,x_{\frac{n}{2}-1}^{2}\) 不构成正负对,也就不能利用对称性求点值。如果能够取到一组构成正负对的点,在子问题中所有正点依然构成正负对,那么就可以继续递推。此时,需要引入复数,例如,取点 \(\pm 1,\pm i\) 构成正负对,子问题中 \(1^{2},i^{2}\) 等价于 \(1,-1\) 依然构成正负对。
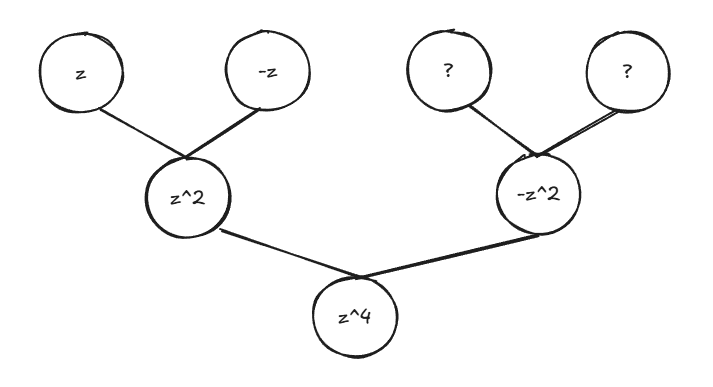
那么对于 \(n-1\) 次多项式,如何取满足条件的 \(n\) 个点?假设取某个点 \(z\),那么必然要取 \(-z\),在子问题中 \(z\) 变为 \(z^{2}\),那么必然要取 \(-z^{2}\),以此类推,假设 \(n\) 为 \(2\) 的幂(总是可以通过对高次项补系数 \(0\) 取到),则最终得到 \(z^{n}\)。也就是说,所有取值的 \(n\) 次方都相等,不妨设 \(z^{n}=1\),求解方程可以得到 \(n\) 个单位根,即为满足条件的 \(n\) 个点。
设复数 \(z=a+bi\),则极坐标表示为 \(z=r(cos(\varphi)+isin(\varphi))\),根据欧拉公式,有 \(z=re^{\varphi i}\)。要求 \(z^{n}=1\),即求 \(r^{n}e^{\varphi ni}=e^{2k\pi i}\),得出 \(r=1,\varphi =\frac{2k\pi}{n}\),所以 \(z=e^{\frac{2k\pi}{n}i}\),其中 \(k=0,1,\cdots,n-1\)。设 \(w_{n}=e^{\frac{2\pi}{n}i}\),则 \(n\) 个单位根分别为 \(w_{n}^{0},w_{n}^{1},\cdots,w_{n}^{n-1}\),它们将复平面中的单位圆 \(n\) 等分。
观察单位根的性质,有 \(w_{n}^{k}=-w_{n}^{k+\frac{n}{2}}\),\(w_{n}^{k}=w_{\frac{n}{2}}^{\frac{k}2}\),所以 \(w_{n}^{0},w_{n}^{1},\cdots,w_{n}^{\frac{n}{2}-1}\) 和 \(w_{n}^{\frac{n}{2}},w_{n}^{\frac{n}{2}+1},\cdots,w_{n}^{n-1}\) 构成正负对。在子问题中,\(w_{n}^{0},w_{n}^{1},\cdots,w_{n}^{\frac{n}{2}-1}\) 变为 \(w_{n}^{0},w_{n}^{2},\cdots,w_{n}^{n-2}\),等价于 \(w_{\frac{n}{2}}^{0},w_{\frac{n}{2}}^{1},\cdots,w_{\frac{n}{2}}^{\frac{n}{2}-1}\),前半和后半依然构成正负对,以此类推。从复平面的角度思考,更容易理解。
根据上述讨论,单位根的正负对性质,在所有子问题中都成立,所以求 \(n-1\) 次多项式 \(P(x)\) 的 \(n\) 个点值,可以使用递归分治的方式求解。当 \(n=1\) 时,多项式是常数,\(P(w_{1}^{0})\) 就是该常数值。当 \(n>1\) 时,如果已知 \(P_{e}(x^{2})\) 和 \(P_{o}(x^{2})\) 在 \(w_{n}^{k}\) 的点值,其中 \(k<\frac{n}{2}\),则利用之前推出的 \(P(x)=P_{e}(x^{2})+xP_{o}(x^{2})\) 公式可以得到以下两个函数值。
优化步骤 ③
步骤 ① 是已知系数,求 \(n-1\) 次多项式 \(P(x)\) 在 \(n\) 个 \(n\) 次单位根位置的值,可以看作矩阵相乘的形式。
步骤 ③ 是已知 \(n\) 个点值,求多项式的系数,可以看作上述变换的逆变换。
如果将步骤 ① 表示为 \(FFT(w_{n},p_{0},p_{1},\cdots,p_{n-1})\),则步骤 ③ 为 \(IFFT(w_{n},P(w_{n}^{0}),P(w_{n}^{1}),\cdots,P(w_{n}^{n-1}))=\frac{1}{n}FFT(w_{n}^{-1},P(w_{n}^{0}),P(w_{n}^{1}),\cdots,P(w_{n}^{n-1}))\)。