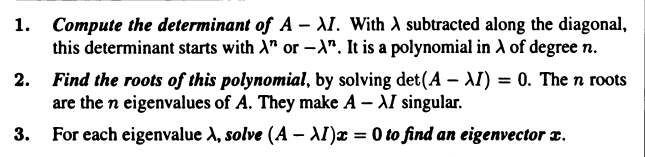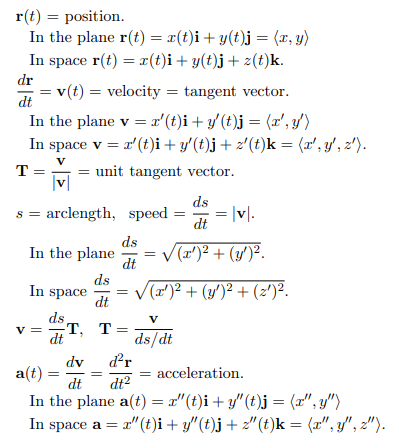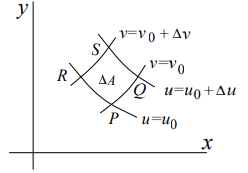参考 Single Variable Calculus,Multivariable Calculus。
Differentiation
Part A: Definition and Basic Rules
几何解释:切线的斜率。物理解释:变化率。如果函数在 \(x_{0}\) 处连续,则 \(\lim_{x\to x_{0}}f(x) = f(x_{0})\)。而极限 \(\lim_{x\to x_{0}}f(x)\) 存在,意味着 \(\lim_{x\to x_{0}^{-}} f(x) = \lim_{x\to x_{0}^{+}} f(x)\)。如果函数在 \(x_{0}\) 处可导,则函数在 \(x_{0}\) 处连续。
$$
f^{\prime}(x) = \lim_{\Delta x\to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}
$$
$$
\lim_{x\to 0}\frac{\sin x}{x} = 1,\
\lim_{x\to 0}\frac{1 - \cos x}{x} = 0
$$
第一类间断点(左右极限都存在):① 跳跃间断点,左右极限存在且不相等;② 可去间断点,左右极限存在且相等,但是函数在该点未定义,或者函数值不等于极限值。第二类间断点(左右极限至少有一个不存在):① 无穷间断点,左右极限为无穷大;② 振荡间断点:左右极限在该点振荡。
$$
(f \pm g)^{\prime} = f^{\prime} \pm g^{\prime},\
(fg)^{\prime} = f^{\prime}g + fg^{\prime},\
(\frac{f}{g})^{\prime} = \frac{f^{\prime}g - fg^{\prime}}{g^{2}},\
(f \circ g)^{\prime}(x) = f^{\prime}(g(x))g^{\prime}(x)
$$
$$
f^{(n)}(x) = \frac{d}{dx}f^{(n - 1)} = \frac{d^{n}f}{dx^{n}} = (\frac{d}{dx})^{n}f = D^{n}f
$$
Part B: Implicit Differentiation and Inverse Functions
对隐函数求导,可以利用链式法则,令 \(u = y^{2}\),则 \(\frac{d}{dx}y^{2} = \frac{du}{dx} = \frac{du}{dy}\frac{dy}{dx} = 2y\frac{dy}{dx}\)。函数 \(f^{-1}(y)\) 是 \(f(x)\) 的反函数,则 \(f^{-1}(f(x)) = x\),原函数和反函数关于 \(y = x\) 对称。根据如下推导,反函数的导数是原函数导数的倒数。
$$
x^{2} + y^{2} = 1 \rightarrow
\frac{d}{dx}(x^{2} + y^{2}) = \frac{d}{dx}(1) \rightarrow
\frac{d}{dx}x^{2} + \frac{d}{dx}y^{2} = 0 \rightarrow
2x + (\frac{d}{dy}y^{2})\frac{dy}{dx} = 0 \rightarrow
2x + 2y\frac{dy}{dx} = 0 \rightarrow
\frac{dy}{dx} = -\frac{x}{y}
$$
$$
y = f(x) \rightarrow
f^{-1}(y) = x \rightarrow
\frac{d}{dx}f^{-1}(y) = \frac{d}{dx}x \rightarrow
\frac{d}{dy}(f^{-1}(y))\frac{d}{dx}y = 1 \rightarrow
\frac{d}{dy}f^{-1}(y) = \frac{1}{\frac{dy}{dx}}
$$
$$
y = \tan^{-1}x \rightarrow
\tan y = x,\ \frac{d}{dy}\tan y = \sec^{2}y \rightarrow
\frac{d}{dx}\tan y = \frac{d}{dx}x \rightarrow
\frac{d}{dy}(\tan y)\frac{d}{dx}y = \frac{d}{dx}x \rightarrow
\frac{dy}{dx} = \cos^{2}y \rightarrow
\frac{dy}{dx} = \frac{1}{1 + x^{2}}
$$
假设某个数 \(e\) 满足 \(M(e) = 1\),定义 \(e^{x}\) 的反函数为 \(\ln x\),则 \(\frac{d}{dx}a^{x} = a^{x}\ln a\)。
$$
\frac{d}{dx}a^{x} = \lim_{\Delta x\to 0}\frac{a^{x + \Delta x} - a^{x}}{\Delta x} =
a^{x}\lim_{\Delta x\to 0}\frac{a^{\Delta x} - 1}{\Delta x} =
a^{x}\left.\frac{d}{dx}a^{x}\right|_{x = 0} = a^{x}M(a) \\
M(e) = 1,\ \frac{d}{dx}e^{x} = e^{x}M(e) = e^{x} \\
\frac{d}{dx}a^{x} = a^{x}M(e^{\ln a}) = a^{x}\ln a
$$
$$
\lim_{x\to \infty}(1 + \frac{1}{x})^{x} \rightarrow
\ln(1 + \frac{1}{x})^{x} = x\ln(1 + \frac{1}{x}) \\
\lim_{x\to \infty}(x\ln(1 + \frac{1}{x})) =
\lim_{\Delta x\to 0}(\frac{1}{\Delta x}\ln(1 + \Delta x)) =
\lim_{\Delta x\to 0}(\frac{1}{\Delta x}(\ln(1 + \Delta x) - \ln 1)) =
\left.\frac{d}{dx}\ln x\right|_{x = 1} = 1 \\
\lim_{x\to \infty}(1 + \frac{1}{x})^{x} =
\lim_{x\to \infty}e^{\ln(1 + \frac{1}{x})^{x}} =
e^{\lim_{x\to \infty}(x\ln(1 + \frac{1}{x}))} =
e
$$
Applications of Differentiation
Part A: Approximation and Curve Sketching
在 \(x = x_{0}\) 附近,有 \(f(x) \approx f(x_{0}) + f^{\prime}(x_{0})(x - x_{0})\)。可以从图像角度理解,切线和函数在该点附近近似。或者从变化率角度理解,\(f^{\prime}(x_{0})(x - x_{0}) = f^{\prime}(x_{0})\Delta x\),即该点的变化率乘以 \(\Delta x\) 就是 \(\Delta f\) 的近似。\(\Delta x\to 0\) 但是不是极限,所以有误差。在 \(x = x_{0}\) 处,泰勒公式和原函数的各阶导数相同。
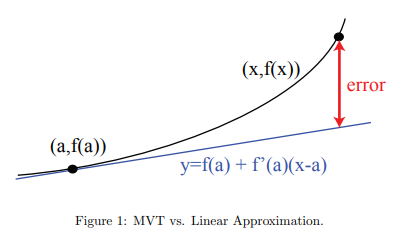
$$
f(x) \approx f(x_{0}) + f^{\prime}(x_{0})(x - x_{0}) + \frac{f^{\prime\prime}(x_{0})}{2!}(x - x_{0})^{2} + \dots + \frac{f^{(n)}(x_{0})}{n!}(x - x_{0})^{n} \quad (x \approx x_{0})
$$
$$
\sin x \approx x,\ \cos x \approx 1,\ e^{x} \approx 1 + x,\ \ln(1 + x) \approx x,\ (1 + x)^{r} \approx 1 + rx \quad (x \approx 0)
$$
$$
\frac{e^{-3x}}{\sqrt{1 + x}} \approx (1 - 3x)(1 - \frac{1}{2}x) \approx 1 - \frac{7}{2}x + \frac{3}{2}x^{2} \approx 1 - \frac{7}{2}x \quad (x \approx 0)
$$
如果 \(f^{\prime} > 0\),则函数递增。如果 \(f^{\prime} < 0\),则函数递减。如果 \(f^{\prime\prime} > 0\),则函数下凸(上凹)。如果 \(f^{\prime\prime} < 0\),则函数上凸(下凹)。当 \(f^{\prime}(x_{0}) = 0\) 时,称 \(x_{0}\) 为驻点,\(f(x_{0})\) 为驻点值。当 \(f^{\prime\prime}(x_{0}) = 0\) 时,且该点两侧二阶导数符号不同,称 \(x_{0}\) 为拐点,\(f(x_{0})\) 为拐点值。
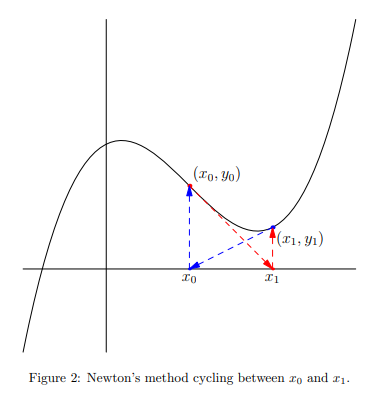
使用牛顿迭代法求方程 \(f(x) = 0\) 的近似解,基本思路是选择接近解的点 \(x_{0}\),然后找到函数 \(f(x)\) 在该点的切线,切线和 \(x\) 轴的交点作为 \(x_{1}\),以此类推,最终 \(x_{n + 1}\) 会收敛到方程 \(f(x) = 0\) 的某个解上。
$$
x_{n + 1} = x_{n} - \frac{f(x_{n})}{f^{\prime}(x_{n})}
$$
牛顿迭代法适用条件:\(x_{0}\) 在解附近,\(|f^{\prime}|\) 不太小,\(|f^{\prime\prime}|\) 不太大。\(|f^{\prime}|\) 太小意味着斜率太小,\(x_{1}\) 距离 \(x_{0}\) 就会很远,导致收敛到其他解上或者无法收敛。\(|f^{\prime\prime}|\) 太大表示斜率变化率太大,该点的切线不能很好的近似函数 \(f\)。
Part C: Mean Value Theorem, Antiderivatives and Differential Equations
中值定理:如果函数 \(f(x)\) 在闭区间 \([a, b]\) 上连续,在开区间 \((a, b)\) 上可导,则在开区间 \((a, b)\) 中至少存在一点 \(c\),使得 \(f^{\prime}© = \frac{f(b) - f(a)}{b - a}\)。对于函数 \(y = f(x)\),\(y\) 的微分是 \(dy = f^{\prime}(x)dx\)。函数 \(g(x)\) 的不定积分是 \(G(x) = \int g(x)dx\)。
$$
\min_{a \leq x \leq b}f^{\prime}(x) \leq \frac{f(b) - f(a)}{b - a} = f^{\prime}(c) \leq \max_{a \leq x \leq b}f^{\prime}(x)
$$
$$
G^{\prime}(x) = g(x),\ dG = g(x)dx
$$
$$
\int x^{n}dx = \frac{x^{n + 1}}{n + 1} + c \quad (n \neq 1),\
\int \frac{1}{x}dx = \ln{|x|} + c
$$
使用换元法求解积分,使用分离变量法求解微分方程。虽然求解得出 \(a > 0\),但是验证之后发现该解对任意 \(a\) 都成立,所以结果不对其做限制。
$$
\begin{align}
\int x^{3}(x^{4} + 2)^{5} &= \int (x^{4} + 2)^{5}x^{3}dx
\quad (u = x^{4} + 2,\ x^{3}dx = \frac{1}{4}du) \\
&= \frac{1}{4}\int u^{5}du = \frac{1}{24}u^{6} + c = \frac{1}{24}(x^{4} + 2)^{6} + c
\end{align}
$$
$$
\frac{dy}{dx} + xy = 0 \rightarrow
\frac{1}{y}dy = -xdx \quad (y \neq 0) \rightarrow
\int \frac{1}{y}dy = \int -xdx \quad (y \neq 0) \rightarrow \\
\ln y = -\frac{1}{2}x^{2} + c \quad (y \gt 0) \rightarrow
y = ae^{-\frac{1}{2}x^{2}} \quad (a = e^{c} \gt 0) \rightarrow
y = ae^{-\frac{1}{2}x^{2}}
$$
The Definite Integral and its Applications
Part A: Definition of the Definite Integral and First Fundamental Theorem
\(\int_{a}^{b}f(x)dx\) 表示函数 \(f(x)\) 在区间 \((a, b)\) 下的面积(有正负)。可以将区间 \((a, b)\) 划分为 \(n\) 等分,计算 \(n\) 个矩形的面积之和(黎曼和),在 \(\lim_{n \to \infty}\) 时得到定积分的值。
$$
\lim_{n \to \infty}\sum_{i = 1}^{n}f(c_{i})\Delta x = \int_{a}^{b}f(x)dx
$$
微积分第一基本定理:如果函数 \(f(x)\) 在区间 \([a, b]\) 上连续,且 \(F^{\prime}(x) = f(x)\),则其满足以下公式。如果 \(f(x) \leq g(x)\) 且 \(a \leq b\),则 \(\int_{a}^{b}f(x)dx \leq \int_{a}^{b}g(x)dx\)。如果 \(u\) 在区间 \(x_{1} \lt x \lt x_{2}\) 是单调的,则 \(\int_{u_{1}}^{u_{2}}g(u)du = \int_{x_{1}}^{x_{2}}g(u(x))u^{\prime}(x)dx\),其中 \(u_{1} = u(x_{1})\)、\(u_{2} = u(x_{2})\)。
$$
\int_{a}^{b}f(x)dx = F(b) - F(a) = \left.F(x)\right|_{a}^{b}
$$
$$
\int_{a}^{b}f(x)dx = -\int_{b}^{a}f(x)dx,\
\int_{a}^{b}f(x)dx + \int_{b}^{c}f(x)dx = \int_{a}^{c}f(x)dx
$$
$$
\int_{-1}^{1}x^{2}dx = \frac{2}{3} \neq \int_{1}^{1}u\frac{1}{2\sqrt u}du = 0 \quad (u = x^{2})
$$
Part B: Second Fundamental Theorem, Areas, Volumes
微积分第二基本定理:如果 \(f(x)\) 在区间 \([a, b]\) 上连续,且 \(G(x) = \int_{a}^{x}f(t)dt\),则 \(G^{\prime}(x) = f(x)\),\(G(a) = 0\)。
$$
F(x) = \int_{0}^{x}e^{-t^{2}}dt,\
\lim_{x \to \infty}F(x) = \frac{\sqrt \pi}{2},\
\lim_{x \to -\infty}F(x) = -\frac{\sqrt \pi}{2} \\
erf(x) = \frac{2}{\sqrt \pi}\int_{0}^{x}e^{-t^{2}}dt = \frac{2}{\sqrt \pi}F(x)
$$
Part C: Average Value, Probability and Numerical Integration
$$
\text{Continuous Average} = \frac{1}{b - a}\int_{a}^{b}f(x)dx = Ave(f)
$$
$$
\text{weighted average} = \frac{\int_{a}^{b}f(x)w(x)dx}{\int_{a}^{b}w(x)dx}
$$
$$
P(x_{1} \lt x \lt x_{2}) = \frac{\int_{x_{1}}^{x_{2}}w(x)dx}{\int_{a}^{b}w(x)dx} =
\frac{\text{Part}}{\text{Whole}} \quad (a \leq x_{1} \lt x_{2} \leq b)
$$
Techniques of Integration
Part A: Trigonometric Powers, Trigonometric Substitution and Completing the Square
$$
\int \sin^{3}xdx = \int (1 - \cos^{2}x)\sin xdx = \int (1 - u^{2})(-du) =
-\cos x + \frac{\cos^{3}x}{3} + c \quad (u = \cos x)
$$
$$
\int \cos^{2}xdx = \int \frac{1 + \cos(2x)}{2}dx = \frac{x}{2} + \frac{\sin(2x)}{4} + c
$$
$$
\sec^{2}x = 1 + \tan^{2}x,\ \frac{d}{dx}\tan x = \sec^{2}x,\ \frac{d}{dx}\sec x = \sec x\tan x
$$
$$
\int \frac{dx}{x^{2}\sqrt{1 + x^{2}}}
= \int \frac{\sec\theta d\theta}{\tan^{2}\theta} \quad (x = \tan\theta)
= \int \frac{\cos\theta d\theta}{\sin^{2}\theta}
= -\frac{1}{u} + c \quad(u = \sin\theta)
= -\csc\theta + c
= -\frac{\sqrt{1 + x^{2}}}{x} + c
$$
Part B: Partial Fractions, Integration by Parts, Arc Length, and Surface Area
使用 Partial Fractions 分解 \(\frac{P(x)}{Q(x)} = \text{quotient} + \frac{R(x)}{Q(x)}\)。如果 \(P(x)\) 的幂次大于等于 \(Q(x)\) 的幂次,则将商提取出来。然后分解 \(Q(x)\),根据以下规则将分子设置为未知数形式,使用 cover-up 方法求解未知数。对于无法这样求解的未知数,则通过对比左右对应幂次项的系数或者直接设置 \(x\) 的值得到方程组,求解方程组得到剩余未知数的解。
$$
\frac{x^{2} + 2}{(x - 1)^{2}(x + 2)}
= \frac{A}{x - 1} + \frac{B}{(x - 1)^{2}} + \frac{C}{x + 2},\
\frac{x^{2}}{(x - 1)(x^{2} + 1)}
= \frac{A}{x - 1} + \frac{Bx + C}{x^{2} + 1},\
\frac{x^{3}}{(x - 1)(x + 2)}
= x - 1 + \frac{3x - 2}{x^{2} + x - 2}
$$
使用分部积分法求积分,需要 \(u\) 的导数更简单,而 \(v\) 的积分不会太复杂。使用勾股定理推出弧长公式。
$$
(uv)^{\prime} = u^{\prime}v + uv^{\prime} \rightarrow
\int uv^{\prime}dx = uv - \int u^{\prime}vdx \\
ds = \sqrt{dx^{2} + dy^{2}} \rightarrow
\text{Arc Length} = \int_{a}^{b}\sqrt{1 + (\frac{dy}{dx})^{2}}dx
$$
$$
\int (\ln x)^{n}dx = x(\ln x)^{n} - n\int(\ln x)^{n - 1}dx \quad (u = (\ln x)^{n},\ v = x) \\
F_{n}(x) = \int (\ln x)^{n}dx \rightarrow F_{n}(x) = x(\ln x)^{n} - nF_{n - 1}(x)
$$
Part C: Parametric Equations and Polar Coordinates
可以将参数方程的变量 \(t\) 看作时间,坐标 \((x(t), y(t))\) 看作轨迹。使用勾股定理推出参数化的弧长公式。
$$
ds = \sqrt{dx^{2} + dy^{2}} \rightarrow
ds = \sqrt{(\frac{dx}{dt})^{2} + (\frac{dy}{dt})^{2}}dt
$$
$$
\left\{\begin{align}
x &= 2\sin t \\
y &= \cos t
\end{align}\right.
\rightarrow
\frac{x^{2}}{4} + y^{2} = 1
\rightarrow
\frac{ds}{dt} = \sqrt{(2\cos t)^{2} + (\sin t)^{2}} = \sqrt{4\cos^{2}t + \sin^{2}t} \\
\text{Arc Length} = \int_{0}^{2\pi}\sqrt{4\cos^{2}t + \sin^{2}t}dt
$$
极坐标使用到原点的距离 \(r\) 和夹角 \(\theta\) 表示平面上的点。使用面积占比等于弧长占比推出面积公式。
$$
x = r\cos\theta,\ y = r\sin\theta,\ r^{2} = x^{2} + y^{2},\ \tan\theta = \frac{y}{x} \\
\frac{dA}{\pi r^{2}} = \frac{d\theta}{2\pi r} \rightarrow
dA = \frac{1}{2}r^{2}d\theta \rightarrow
A = \int_{\theta_{1}}^{\theta_{2}}\frac{1}{2}r^{2}d\theta
$$
Exploring the Infinite
Part A: L’Hospital’s Rule and Improper Integrals
使用洛必达法则求解 \(0/0\) 和 \(\infty/\infty\) 型未定式 \(\lim_{x\to a}\frac{f(x)}{g(x)} = \lim_{x\to a}\frac{f^{\prime}(x)}{g^{\prime}(x)}\)。如果 \(p \gt 0\),当 \(x \to \infty\) 有 \(\ln x \ll x^{p} \ll e^{x}\)。
$$
\lim_{x \to a}\frac{f(x)}{g(x)}
= \lim_{x \to a}\frac{f(x)/(x - a)}{g(x)/(x - a)}
= \frac{\lim_{x \to a}(f(x)/(x - a))}{\lim_{x \to a}(g(x)/(x - a))}
= \frac{\lim_{x \to a}\frac{f(x) - f(a)}{x - a}}{\lim_{x \to a}\frac{g(x) - g(a)}{x - a}}
\quad (f(a) = g(a) = 0)
= \frac{f^{\prime}(a)}{g^{\prime}(a)}
$$
$$
\lim_{x \to 0^{+}}x^{x}
= e^{\lim_{x \to 0^{+}}x\ln x}
= e^{\lim_{x \to 0^{+}}\frac{\ln x}{\frac{1}{x}}}
= e^{\lim_{x \to 0^{+}}-x}
= e^{0}
= 1
$$
函数 \(f(x) \gt 0\) 的反常积分为 \(\int_{a}^{\infty}f(x)dx = \lim_{N \to \infty}\int_{a}^{N}f(x)dx\),如果极限存在,则反常积分收敛,否则发散。
$$
\int_{0}^{\infty}e^{-kx}dx = \frac{1}{k},\
\int_{-\infty}^{\infty}e^{-x^{2}}dx = \sqrt \pi,\
\int_{1}^{\infty}\frac{dx}{x^{p}}
= \frac{\infty^{-p + 1}}{-p + 1} + \frac{1}{p - 1} \quad (p \neq 1)
$$
$$
\int_{-1}^{1}\frac{dx}{x^{2}}
= \int_{-1}^{0}\frac{dx}{x^{2}} + \int_{0}^{1}\frac{dx}{x^{2}}
= \infty \neq \left.-x^{-1}\right|_{-1}^{1} = -2
$$
Part B: Taylor Series
如果 \(f(x)\) 在区间 \([1, \infty]\) 递减且 \(f(x) > 0\),则 \(\sum_{1}^{\infty}f(n)\) 和 \(\int_{1}^{\infty}f(x)dx\) 同时收敛或发散,其满足如下公式。如果 \(f(n) \sim g(x)\)(\(\lim_{n \to \infty}\frac{f(n)}{g(n)} = 1\)),且对于所有 \(n\) 都有 \(g(n) \gt 0\),则 \(\sum_{n = 1}^{\infty}f(n)\) 和 \(\sum_{n = 1}^{\infty}g(n)\) 同时收敛或发散。
$$
\sum_{1}^{\infty}f(n) - \int_{1}^{\infty}f(x)dx < f(1)
$$
$$
\sum_{n = 0}^{\infty}x^{n} = \frac{1}{1 - x} \quad (|x| \lt 1),\
\sum_{n = 1}^{\infty}\frac{1}{n^{2}} = \frac{\pi^{2}}{6},\
\lim_{N \to \infty}\ln N \lt
\sum_{n = 1}^{\infty}\frac{1}{n} = \infty
\lt \lim_{N \to \infty}\ln N + 1
$$
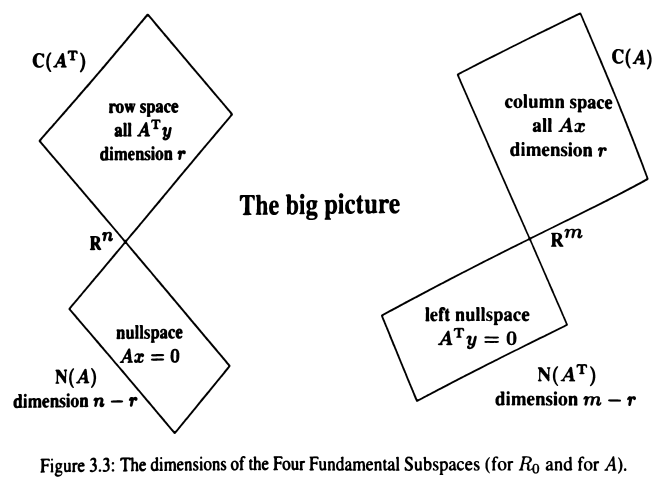
Vectors and Matrices
Part A: Vectors, Determinants, and Planes
向量可以被视作位移,\(\vec{PQ} = \vec{Q} - \vec{P}\) 表示从点 \(P\) 到 \(Q\) 的位移。使用余弦定理证明点积的代数和几何表示等价。如果 \(\hat u\) 是单位向量,则向量 \(A\) 在 \(\hat u\) 方向上的分量是 \(A \cdot \hat u = |A|\cos\theta\)(分量是标量)。两个向量的叉乘仍是向量,方向垂直于两个向量所在的平面,符合右手定则。使用拉格朗日恒等式推出叉乘的几何表示。
$$
|A - B|^{2} = |A|^{2} + |B|^{2} + 2|A||B|\cos\theta \rightarrow
A \cdot B = ac - bd = |A||B|\cos\theta
$$
$$
\text{Area} = |\det(A, B)|,\ \text{Volume} = |\det(A, B, C)|
$$
$$
A \times B =
\left|\begin{matrix}
i & j & k \\
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3}
\end{matrix}\right|
=
i
\left|\begin{matrix}
a_{2} & a_{3} \\
b_{2} & b_{3}
\end{matrix}\right|
-
j
\left|\begin{matrix}
a_{1} & a_{3} \\
b_{1} & b_{3}
\end{matrix}\right|
+
k
\left|\begin{matrix}
a_{1} & a_{2} \\
b_{1} & b_{2}
\end{matrix}\right|
=
\langle a_{2}b_{3} - a_{3}b_{2}, a_{3}b_{1} - a_{1}b_{3}, a_{1}b_{2} - a_{2}b_{1} \rangle
$$
$$
|A \times B|^{2} = |A|^{2}|B|^{2} - (A \cdot B)^{2} \rightarrow
|A \times B| = |A||B|\sin\theta
$$
Part B: Matrices and Systems of Equations
$$
A =
\left[\begin{matrix}
4 & 1 \\
1 & 3
\end{matrix}\right]
, i =
\left[\begin{matrix}
1 \\ 0
\end{matrix}\right]
, j =
\left[\begin{matrix}
0 \\ 1
\end{matrix}\right]
\rightarrow
Ai =
\left[\begin{matrix}
4 \\ 1
\end{matrix}\right]
, Aj =
\left[\begin{matrix}
1 \\ 3
\end{matrix}\right]
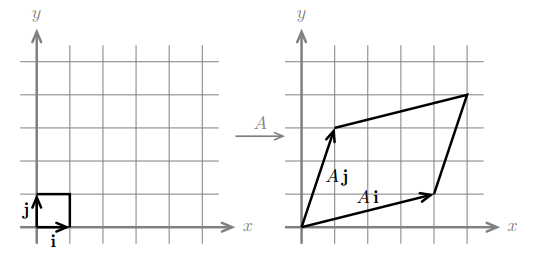
$$
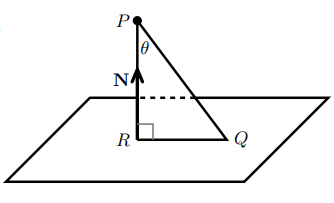
如果已知平面上的点 \(P_{0} = (x_{0}, y_{0}, z_{0})\) 和法向量 \(\vec{N} = \langle a, b, c \rangle\),设 \(P = (x, y, z)\) 为平面上任意点,则平面方程如下。
$$
N \cdot \vec{P_{0}P} = 0 \iff a(x - x_{0}) + b(y - y_{0}) + c(z - z_{0}) = 0
$$
$$
d = |PR| = |\vec{PQ}|\cos\theta = \left|\vec{PQ} \cdot \frac{N}{|N|}\right|
$$
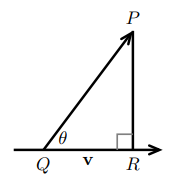
$$
d = |\vec{QP}|\sin\theta = \left|\vec{QP} \times \frac{v}{|v|}\right|
$$
Part C: Parametric Equations for Curves
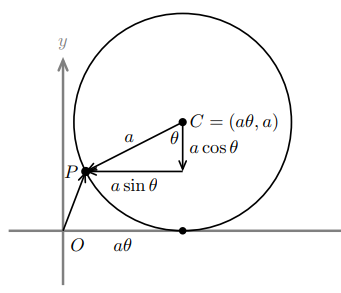
如果直线过点 \(P_{0} = (x_{0}, y_{0}, z_{0})\),且和向量 \(\vec{v} = \langle v_{1}, v_{2}, v_{3} \rangle\) 的方向相同,则直线的参数方程如下。圆、抛物线和摆线的参数方程也在下面列出。将 \(t\) 看作时间,则位置、速度(切向量)、速率和加速度的关系如下。
$$
r(t)
= \langle x, y, z \rangle
= \vec{OP_{0}} + tv
= \langle x_{0} + tv_{1}, y_{0} + tv_{2}, z_{0} + tv_{3} \rangle
$$
$$
x(t) = a\cos t, y(t) = a\sin t \quad
x(t) = a\cos t, y(t) = b\cos t \quad
x(\theta) = a\theta - a\sin\theta, y(\theta) = a - a\cos\theta
$$
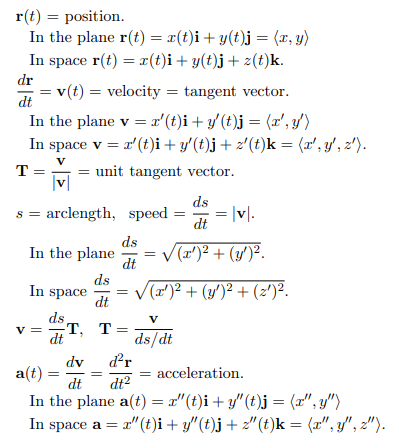
Partial Derivatives
Part A: Functions of Two Variables, Tangent Approximation and Optimization
对于函数 \(w = f(x, y)\),当固定 \(y = y_{0}\) 时,得到偏函数 \(w = f(x, y_{0})\)。该偏函数在 \(x = x_{0}\) 处的导数就是函数 \(f\) 在 \((x_{0}, y_{0})\) 处的偏导数,表示当 \(y = y_{0}\) 时,\(w\) 关于 \(x\) 的变化率。该函数在点 \((x_{0}, y_{0}, w_{0})\) 处的切平面,必然包含两个偏函数在该点的切线,其方程如下所示。如果在 \((x_{0}, y_{0})\) 附近,偏函数 \(f_{x}\) 和 \(f_{y}\) 连续,则在该点附近切平面近似曲线。
$$
\left.\frac{d}{dx}f(x, y_{0})\right|_{x_{0}}
= \left.\frac{\partial f}{\partial x}\right|_{(x_{0}, y_{0})}
= \left.\frac{\partial w}{\partial x}\right|_{(x_{0}, y_{0})}
= \left(\frac{\partial f}{\partial x}\right)_{0}
= \left(\frac{\partial w}{\partial x}\right)_{0}
= f_{x}(x_{0}, y_{0})
$$
$$
A(x - x_{0}) + B(y - y_{0}) + C(w - w_{0}) = 0 \rightarrow
w - w_{0} = a(x - x_{0}) + b(y - y_{0}) \quad
(C \neq 0, a = \frac{A}{C} = \left(\frac{\partial w}{\partial x}\right)_{0}, b = \frac{B}{C} = \left(\frac{\partial w}{\partial y}\right)_{0}
$$
$$
f(x, y) \approx w_{0} + \left(\frac{\partial w}{\partial x}\right)_{0}(x - x_{0}) + \left(\frac{\partial w}{\partial y}\right)_{0}(y - y_{0}) \iff \Delta w \approx \left(\frac{\partial w}{\partial x}\right)_{0}\Delta x + \left(\frac{\partial w}{\partial y}\right)_{0}\Delta y \quad (\Delta x, \Delta y \approx 0)
$$
极值点处的切平面水平,有 \(f_{x} = 0\) 和 \(f_{y} = 0\),但是满足该条件的点不一定是极值点。最小二乘法拟合直线 \(y = ax + b\),需要最小化 \(D = \sum_{i = 1}^{n}(y_{i} - (ax_{i} + b))^{2}\),相当于求 \(D = f(a, b)\) 的极值点,令各个偏导为零可以推出如下方程组。
$$
\left\{\begin{align}
\bar{s}a + \bar{x}b &= \frac{1}{n}\sum{x_{i}y_{i}} \\
\bar{x}a + b &= \bar{y}
\end{align}\right.
\quad (\bar{s} = \sum{\frac{x_{i}^{2}}{n}})
$$
对于单变量函数 \(f(x)\),如果 \(f^{\prime}(x_{0}) = 0\) 且 \(f^{\prime\prime}(x_{0}) \gt 0\),则 \(x_{0}\) 是局部最小值点,而 \(f^{\prime\prime}(x_{0}) \lt 0\) 则为局部最大值点。基本想法是,二阶导数大于零或小于零则一阶导数递增或递减,说明该点两侧的一阶导数符号不同,该点局部最小或最大。对于多变量函数 \(f(x, y)\),假设导数存在且连续,令各个偏导为零,求得临界点 \((x_{0}, y_{0})\),然后通过以下测试判断该点是否是极值点。
$$
(f)_{0} = f(x_{0}, y_{0}),\ A = (f_{xx})_{0},\ B = (f_{xy})_{0} = (f_{yx})_{0},\ C = (f_{yy})_{0}
$$

Part B: Chain Rule, Gradient and Directional Derivatives
如果 \(w = f(x, y), x = x(u, v), y = y(u, v)\),\(u, v\) 是自变量,\(x, y\) 是中间变量,\(w\) 是因变量,根据切平面近似公式可以推出偏导满足链式法则。同样根据近似公式,得出函数 \(w = f(x, y)\) 的全微分为 \(dw = f_{x}dx + f_{y}dy\)。
$$
\Delta w \approx \left.\frac{\partial w}{\partial x}\right|_{0}\Delta x + \left.\frac{\partial w}{\partial y}\right|_{0}\Delta y
\rightarrow
\frac{\Delta w}{\Delta u} \approx \left.\frac{\partial w}{\partial x}\right|_{0}\frac{\Delta x}{\Delta u} + \left.\frac{\partial w}{\partial y}\right|_{0}\frac{\Delta y}{\Delta u}
\rightarrow
\frac{\partial w}{\partial u} = \frac{\partial w}{\partial x}\frac{\partial x}{\partial u} + \frac{\partial w}{\partial y}\frac{\partial y}{\partial u}
\quad (\Delta x, \Delta y \approx 0)
$$
如果 \(w = f(x, y)\),则 \(\frac{\partial w}{\partial x}\) 和 \(\frac{\partial w}{\partial y}\) 是 \(w\) 在向量 \(i\) 和 \(j\) 方向上的变化率,这两个偏导组成的向量就是 \(w\) 的梯度,梯度和等值线垂直。求 \(x^{2} + 2y^{2} + 3z^{2} = 6\) 在点 \(P = (1, 1, 1)\) 的切平面,可以先求 \(w = x^{2} + 2y^{2} + 3z^{2}\) 在等值面 \(w = 6\) 的梯度,该梯度和等值面垂直也就和切平面垂直,所以可以使用点法式得出切平面的方程 \(2(x - 1) + 4(y - 1) + 6(z - 1) = 0\)。
$$
\text{grad } w
= \nabla w
= \left\langle\frac{\partial w}{\partial x}, \frac{\partial w}{\partial y}\right\rangle
$$
函数 \(w = f(x, y)\) 在点 \(P_{0}\) 处沿单位向量 \(u\) 方向的导数如下,其中 \(\Delta w\) 表示沿 \(u\) 方向移动 \(\Delta s\) 距离之后 \(w\) 的变化量,单位向量 \(u\) 在 \(xy\) 平面中。梯度 \(\nabla w\) 的方向就是 \(w\) 变化率最大的方向,方向导数就是梯度在 \(u\) 方向上的投影大小。
$$
\left\{\begin{align}
(\Delta s)^{2} = (\Delta x)^{2} + (\Delta y)^{2} &\rightarrow
u = \left\langle\frac{\Delta x}{\Delta s}, \frac{\Delta y}{\Delta s}\right\rangle \\
\Delta w \approx \left(\frac{\partial w}{\partial x}\right)_{0}\Delta x + \left(\frac{\partial w}{\partial y}\right)_{0}\Delta y &\rightarrow
\frac{\Delta w}{\Delta s} \approx \left(\frac{\partial w}{\partial x}\right)_{P_{0}}\frac{\Delta x}{\Delta s} + \left(\frac{\partial w}{\partial y}\right)_{P_{0}}\frac{\Delta y}{\Delta s}
\end{align}\right.
\rightarrow
\left.\frac{dw}{ds}\right|_{P_{0}, u}
= \lim_{\Delta s \to 0}\frac{\Delta w}{\Delta s}
= \left.\nabla w\right|_{P_{0}} \cdot u
$$
$$
\left.\frac{dw}{ds}\right|_{u}
= \nabla w \cdot u
= |\nabla w||u|\cos\theta
= |\nabla w|\cos\theta
$$
Part C: Lagrange Multipliers and Constrained Differentials
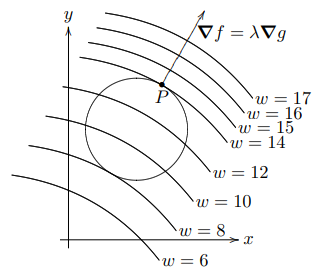
拉格朗日乘数问题:最小化或最大化 \(w = f(x, y, z)\),且满足约束条件 \(g(x, y, z) = c\)。解决方案:局部最小值或最大值必定出现在临界点上,该点满足 \(\nabla f = \lambda\nabla g\)(两个梯度平行)和 \(g(x, y, z) = c\)。对于函数 \(w = f(x, y, z, t)\),\(\left(\frac{\partial w}{\partial x}\right)_{y, t}\) 表示 \(w\) 关于 \(x\) 的偏导,其中 \(x, y, t\) 是自变量,\(z\) 是因变量,\(y, t\) 视为常量。
$$
\left(\frac{\partial x}{\partial y}\right)_{z}\left(\frac{\partial y}{\partial x}\right)_{z} = 1,\
\left(\frac{\partial x}{\partial y}\right)_{z}\left(\frac{\partial y}{\partial t}\right)_{z} = \left(\frac{\partial x}{\partial t}\right)_{z},\
\left(\frac{\partial x}{\partial y}\right)_{z}\left(\frac{\partial y}{\partial z}\right)_{x}\left(\frac{\partial z}{\partial x}\right)_{y} = -1
$$
Double Integrals and Line Integrals in the Plane
Part A: Double Integrals
函数 \(f(x, y)\) 在平面区域 \(R\) 上的二重积分如下。将区域 \(R\) 分为 \(n\) 份,假设第 \(i\) 份的面积为 \(\Delta A_{i}\),点 \((x_{i}, y_{i})\) 在其中,则该二重积分可以看作以曲面 \(f(x, y)\) 为顶,区域 \(R\) 为底的曲顶柱体的体积。
$$
\int\int_{R}f(x, y)dA
= \lim_{\Delta A \to 0}\sum_{i = 1}^{n}f(x_{i}, y_{i})\Delta A_{i}
$$
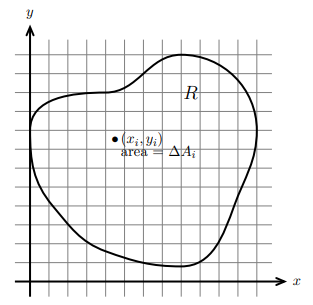
计算区域 \(R\) 的二重积分的步骤如下,假设先对 \(y\) 积分再对 \(x\) 积分:将 \(x\) 固定,沿 \(y\) 递增的方向做垂线,积分的下限和上限就是垂线进入和离开区域 \(R\) 时对应的 \(y\) 值;然后让 \(x\) 递增,积分的下限和上限就是垂线和区域 \(R\) 相交的最小和最大 \(x\) 值。先对 \(x\) 积分再对 \(y\) 积分的形式同理,极坐标中的二重积分也是这样计算的。
$$
\int\int_{R}f(x, y)dydx
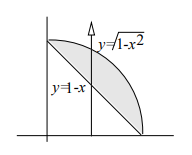
= \int_{0}^{1}\int_{1 - x}^{\sqrt{1 - x^{2}}}f(x, y)dydx
= \int_{0}^{1}\int_{1 - y}^{\sqrt{1 - y^{2}}}f(x, y)dxdy
$$
$$
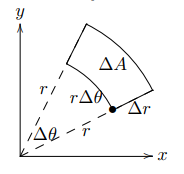
dA = rdrd\theta
$$
质心是位置根据质量的加权平均值,对于连续的线段或区域,其质量和质心的公式如下,其中 \(\delta\) 是密度函数。
$$
M = \int_{a}^{b}\delta(x)dx,\
x_{cm} = \frac{1}{M}\int_{a}^{b}x\delta(x)dx \\
M = \int\int_{R}\delta(x, y)dA,\
x_{cm} = \frac{1}{M}\int\int_{R}x\delta(x, y)dA,\
y_{cm} = \frac{1}{M}\int\int_{R}y\delta(x, y)dA
$$
二重积分的换元步骤:使用 \(u = u(x, y), v = v(x, y)\) 将 \(f(x, y)\) 替换为 \(g(u, v)\),使用 Jacobian 行列式得到由 \(dudv\) 表示的 \(dA\),根据区域 \(R\) 得到积分的上下限。面积 \(dA\) 的推导过程如下,求解 \(PQ\) 的 \(\Delta x\) 时,固定 \(v = v_{0}\) 不变,此时 \(x\) 可以看作关于 \(u\) 的单变量函数,\(\Delta x\) 就是 \(x\) 在 \(u\) 方向上的变化率(偏导)乘以 \(\Delta u\)。
$$
\frac{\partial(x, y)}{\partial(u, v)} =
\left|\begin{matrix}
x_{u} & x_{v} \\
y_{u} & y_{v}
\end{matrix}\right|,\
dA = \left|\frac{\partial(x, y)}{\partial(u, v)}\right|dudv,\
\int\int_{R}f(x, y)dxdy = \int\int_{R}g(u, v)\left|\frac{\partial(x, y)}{\partial(u, v)}\right|dudv
$$
$$
PQ = \Delta xi + \Delta yj
\approx \left(\frac{\partial x}{\partial u}\right)_{0}\Delta u\mathbf{i} + \left(\frac{\partial y}{\partial u}\right)_{0}\Delta u\mathbf{j} \\
PR = \Delta xi + \Delta yj
\approx \left(\frac{\partial x}{\partial v}\right)_{0}\Delta v\mathbf{i} + \left(\frac{\partial y}{\partial v}\right)_{0}\Delta v\mathbf{j} \\
\Delta A \approx \text{area of parallelogram PQRS} = |PQ \times PR| =
\left|\begin{matrix}
x_{u} & x_{v} \\
y_{u} & y_{v}
\end{matrix}\right|_{0}
\Delta u \Delta v \rightarrow
dA = \left|\frac{\partial(x, y)}{\partial(u, v)}\right|dudv
$$
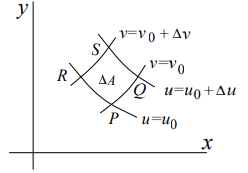
有时根据 \(u = u(x, y), v = v(x, y)\) 求解 \(x = x(u, v), y = y(u, v)\) 比较困难,此时可以使用以下公式求解 \(\frac{\partial(x, y)}{\partial(u, v)}\)。如果区域 \(R\) 不是由 \(u, v\) 的等值线围成,那么积分的上下限就不是常数,此时需要找到边界关于 \(uv\) 的方程。
$$
\frac{\partial(x, y)}{\partial(u, v)}\frac{\partial(u, v)}{\partial(x, y)} = 1
$$
Part B: Vector Fields and Line Integrals