参考 Introduction to Probability,MIT 6.041SC FALL 2013,Probability Cheatsheet。
Unit I: Probability Models And Discrete Random Variables
Lecture 2: Conditioning and Bayes’ Rule
条件概率 \(P(A \mid B)\) 表示在 \(B\) 发生的前提下 \(A\) 发生的概率,此时 \(B\) 作为全集,\(A\) 在 \(B\) 中的占比就是该条件概率的值。如果乘以 \(P(B)\) 就是将 \(\Omega\) 作为全集,自然会得到 \(P(A \cap B)\)。反之, 将 \(P(A \cap B)\) 除以 \(P(B)\) 就是将全集 \(\Omega\) 缩减为 \(B\),从而得到条件概率 \(P(A \mid B)\),此时要求 \(P(B) \neq 0\)。
$$
P(A \cap B) = P(B)P(A \mid B) = P(A)P(B \mid A)
$$
$$
P(B) = P(A)P(B \mid A) + P(A^{c})P(B \mid A^{c})
$$
$$
P(A_{i} \mid B)
= \frac{P(A_{i} \cap B)}{P(B)}
= \frac{P(A_{i})P(B \mid A_{i})}{P(B)}
= \frac{P(A_{i})P(B \mid A_{i})}{\sum_{j}P(A_{j})P(B \mid A_{j})}
$$
Lecture 3: Independence
如果 \(A\) 和 \(B\) 独立,则 \(P(B \mid A) = P(B)\),\(P(A \cap B) = P(A)P(B)\)。如果 \(A\) 和 \(B\) 互斥,则 \(P(A \cap B) = 0\)。如果 \(P(A), P(B) \gt 0\),互斥必然不独立,独立必然不互斥。如果 \(A\) 和 \(B\) 独立,则其在 \(C\) 发生的前提下不一定独立,即独立不意味着条件独立。如果 \(A, B, C\) 两两独立,不意味着 \(A, B, C\) 独立。
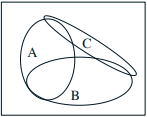
例如,假设抛两次硬币,\(A\) 表示第一次是正面,\(B\) 表示第二次是正面,这两个事件是独立的。如果 \(C\) 表示两次同面,则在 \(C\) 发生的前提下 \(A\) 和 \(B\) 不独立。此时 \(A, B, C\) 两两独立,但是 \(P(A \cap B \cap C) \neq P(A)P(B)P©\),即 \(A, B, C\) 不独立。如果两次中有一次是正面,则另一次是反面的概率是多少?答案是 \(\frac{2}{3}\) 而不是 \(\frac{1}{2}\),虽然 \(A\) 和 \(B\) 独立,但是原始样本空间的大小是 \(4\) 而不是 \(2\),这个需要特别注意。
Lecture 4: Counting
包含 \(n\) 个元素的集合,有 \(n!\) 个排列,\(2^{n}\) 个子集。从中选择 \(k\) 个元素,有 \(\binom{n}{k} = \frac{n!}{(n - k)!k!}\) 种情况,除以 \(k!\) 表示去除相同元素不同排列的情况。将 \(52\) 张牌平均分成 \(4\) 份,每份中都有 \(A\) 的概率是多少?答案是 \(\frac{13^{4}}{C_{52}^{4}}\),表示从 \(52\) 个位置选择 \(4\) 个位置放 \(A\),符合条件的情况是每 \(13\) 个位置选择 \(1\) 个位置放 \(A\)。另一个办法是,将 \(52\) 张牌均分,符合条件的情况是单独分 \(A\) 再将 \(48\) 张牌均分,得到 \(\frac{4!C_{48}^{12}C_{36}^{12}C_{24}^{12}C_{12}^{12}}{C_{52}^{13}C_{39}^{13}C_{26}^{13}C_{13}^{13}}\),化简之后和上述答案相同。
$$
(a + b)^{n} = \sum_{k = 0}^{n}\binom{n}{k}a^{k}b^{n - k}
$$
Lecture 5: Discrete Random Variables; Probability Mass Functions; Expectations
随机变量是函数,将样本空间 \(\Omega\) 映射到实数。如下概率质量函数(PMF),表示随机变量 \(X\) 的值为 \(x\) 的概率。例如,假设抛一次硬币是正面的概率为 \(P(H) = p\),则抛 \(n\) 次硬币有 \(k\) 次是正面的 PMF 为 \(p_{X}(k) = \binom{n}{k}p^{k}(1 - p)^{n - k}\)(二项分布的 PMF),随机变量 \(X\) 将抛 \(n\) 次硬币的样本空间映射到硬币是正面的次数,\(n\) 越大该函数图像越接近钟型曲线。如果连续抛硬币直到正面为止,则抛 \(k\) 次才停止的 PMF 为 \(p_{X}(k) = (1 - p)^{k - 1}p\)(几何分布的 PMF)。
$$
p_{X}(x)
= P(X = x)
= P(\{\omega \in \Omega\ \text{s.t.}\ X(\omega) = x\}),\
p_{X}(x) \geq 0,\
\sum_{x}p_{X}(x) = 1
$$
随机变量 \(X\) 的期望为 \(E[x] = \sum_{x}xp_{X}(x)\),可以将概率 \(p_{X}(x)\) 视为 \(x\) 出现的频率,期望视为 \(x\) 根据概率的加权平均值,或者将期望看作 PMF 的重心。假设随机变量 \(Y\) 是关于随机变量 \(X\) 的函数 \(Y = g(X)\),则有如下公式计算 \(Y\) 的期望(无意识统计学家法则,LOTUS)。通常情况下 \(E[g(X)] \neq g(E[X])\),除非 \(g\) 是线性函数。方差(Variance)是随机变量和自身期望的偏差平方的期望,用于描述随机变量的离散程度。
$$
E[y] = \sum_{y}yp_{Y}(y) = \sum_{x}g(x)p_{X}(x) \quad (Y = g(X))
$$
$$
E[\alpha] = \alpha,\
E[\alpha X] = \alpha E[X],\
E[\alpha X + \beta] = \alpha E[x] + \beta
\quad (\alpha, \beta \text{ are constants})
$$
$$
\DeclareMathOperator{\var}{var}
E[X^{2}] = \sum_{x}x^{2}p_{X}(x),\
E[X - E[x]] = E[x] - E[x] = 0 \\
\var(X) = E[(X - E[X])^{2}] = \sum_{x}(x - E[x])^{2}p_{X}(x) = E[X^{2}] - (E[X])^{2} \\
\var(X) \geq 0,\
\var(\alpha X + \beta) = \alpha^{2}\var(X),\
\sigma_{X} = \sqrt{\var(X)}
$$
Lecture 6: Discrete Random Variable Examples; Joint PMFs
随机变量 \(X\) 的条件 PMF 为 \(p_{X \mid A}(x) = P(X = x \mid A)\),条件期望为 \(E[X \mid A] = \sum_{x}xp_{X \mid A}(x)\)。几何分布的期望为 \(E[X] = \sum_{k = 1}^{\infty}k(1 - p)^{k - 1}p\),几何分布具有无记忆性(Memoryless),\(p_{X - 2 \mid X \gt 2}(k) = p_{X}(k)\),过去发生的事情不会影响未来发生的事情。结合几何分布的无记忆性和如下全期望定理可以推出几何分布的期望为 \(E[X] = \frac{1}{p}\),使用错位相减化简或者对几何级数求导也可以得到该结果。
$$
P(B) = P(A_{1})P(B \mid A_{1}) + \cdots + P(A_{n})P(B \mid A_{n})
$$
$$
p_{X}(x) = P(A_{1})p_{X \mid A_{1}}(x) + \cdots + P(A_{n})p_{X \mid A_{n}}(x) \rightarrow
E[X] = P(A_{1})E[X \mid A_{1}] + \cdots + P(A_{n})E[X \mid A_{n}]
$$
$$
E[X] = P(X = 1)E[X \mid X = 1] + P(X \gt 1)E[X \mid X \gt 1] \rightarrow
E[x] = p \cdot 1 + (1 - p) \cdot (E[X] + 1) \rightarrow
E[x] = \frac{1}{p}
$$
随机变量 \(X\) 和 \(Y\) 的联合 PMF 为 \(p_{X, Y}(x, y) = P(X = x, Y = y)\),满足以下性质。可以通过联合 PMF 得到单个随机变量的边缘 PMF,条件 PMF 表示在 \(Y = y\) 的前提下 \(X = x\) 的概率,除以 \(p_{Y}(y)\) 将全集缩减到 \(Y = y\) 的情况。条件 PMF 和普通 PMF 相同,概率求和得到 \(1\)。
$$
\sum_{x}\sum_{y}p_{X, Y}(x, y) = 1,\
p_{X}(x) = \sum_{y}p_{X, Y}(x, y),\
p_{X \mid Y}(x \mid y) = P(X = x \mid Y = y) = \frac{p_{X, Y}(x, y)}{p_{Y}(y)},\
\sum_{x}p_{X \mid Y}(x \mid y) = 1
$$
Lecture 7: Multiple Discrete Random Variables
如果随机变量 \(X, Y, Z\) 独立,则 \(p_{X, Y, Z} = p_{X}(x) \cdot p_{Y}(y) \cdot p_{Z}(x)\),此时 \(p_{X \mid Y, Z}(x \mid y, z) = p_{X}(x)\)。
$$
P(A \cap B \cap C) = P(A)P(B \mid A)P(C \mid A \cap B) \rightarrow
p_{X, Y, Z}(x, y, z) = p_{X}(x)p_{Y \mid X}(y \mid x)p_{Z \mid X, Y}(z \mid x, y)
$$
$$
E[g(X, Y)] = \sum_{x}\sum_{y}g(x, y)p_{X, Y}(x, y),\
E[X + Y + Z] = E[X] + E[Y] + E[Z]
$$
$$
\DeclareMathOperator{\var}{var}
E[XY] = E[X]E[Y],\
E[g(X)h(Y)] = E[g[X]]e[h(Y)],\
\var(X + Y) = \var(X) + \var(Y)
\quad (X, Y \text{ are independent})
$$
二项分布的期望和方差如下,有 \(X = \sum_{i = 1}^{n}X_{i}\),其中 \(X_{i}\) 表示第 \(i\) 次试验是否成功的指示变量。
$$
\DeclareMathOperator{\var}{var}
E[X] = \sum_{k = 0}^{n}k\binom{n}{k}p^{k}(1 - p)^{n - k},\
E[X_{i}] = 1 \cdot p + 0 \cdot (1 - p) = p,\
E[X] = \sum_{i = 1}^{n}E[X_{i}] = np \\
\var(X_{i}) = p(1 - p)^{2} + (1 - p)(0 - p)^{2} = E[X_{i}^{2}] - E[X_{i}]^{2} = p(1 - p),\
\var(X) = \sum_{i = 1}^{n}\var(X_{i}) = np(1 - p)
$$
Unit II: General Random Variables
Lecture 8: Continuous Random Variables
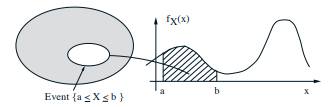
连续型随机变量由概率密度函数(PDF)\(f_{X}\) 描述,密度(函数值)不是概率,该函数和 \(x\) 轴围成的面积才是概率。和 PMF 不同,PDF 在某点的概率总是零,因为面积是零。连续型和离散型随机变量的累积分布函数(CDF)\(F(x)\) 如下所示,连续型随机变量的 CDF 的导数等于密度,即密度是 CDF 的变化率。
$$
P(a \leq X \leq b) = \int_{a}^{b}f_{X}(x)dx,\
f_{X} \geq 0,\
\int_{-\infty}^{\infty}f_{X}(x)dx = 1,\
P(x \leq X \leq x + \delta) = \int_{x}^{x + \delta}f_{X}(s)ds \approx f_{X}(x) \cdot \delta
$$
$$
\DeclareMathOperator{\var}{var}
E[X] = \int_{-\infty}^{\infty}xf_{X}(x)dx,\
E[g(X)] = \int_{-\infty}^{\infty}g(x)f_{X}(x)dx,\
\var(X) = \sigma_{X}^{2} = \int_{-\infty}^{\infty}(x - E[X])^{2}f_{X}(x)dx
$$
$$
F_{X}(x) = P(X \leq x) = \int_{-\infty}^{x}f_{X}(t)dt,\
F_{X}(x) = P(X \leq x) = \sum_{k \leq x}p_{X}(k)
$$
正态分布(高斯分布)的 PDF 如下所示。标准正态分布的均值为 \(0\),方差为 \(1\)。一般正态分布的均值为 \(\mu\),方差为 \(\sigma^{2}\),相当于将函数图像向右移动 \(\mu\),然后 \(\sigma\) 越小图像越窄,因为 \(e\) 的指数降低得更快。系数 \(\frac{1}{\sqrt{2\pi}}\) 和 \(\frac{1}{\sigma\sqrt{2\pi}}\) 确保 PDF 在整个实数域上的积分是 \(1\)。如果 \(X \sim N(\mu, \sigma^{2})\),则 \(\frac{X - \mu}{\sigma} \sim N(0, 1)\)。
$$
\DeclareMathOperator{\var}{var}
f_{X}(x) = \frac{1}{\sqrt{2\pi}}e^{-x^{2} / 2},\
E[X] = 0,\
\var(X) = 1
\quad N(0, 1)
$$
$$
\DeclareMathOperator{\var}{var}
f_{X}(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-(x - \mu)^{2} / 2\sigma^{2}},\
E[X] = \mu,\
\var(X) = \sigma^{2}
\quad N(\mu, \sigma^{2})
$$
$$
\DeclareMathOperator{\var}{var}
X \sim N(\mu, \sigma^{2}),\
Y = aX + b \rightarrow
E[Y] = a\mu + b,\
\var(Y) = a^{2}\sigma^{2},\
Y \sim N(a\mu + b, a^{2}\sigma^{2})
$$
Lecture 9: Multiple Continuous Random Variables
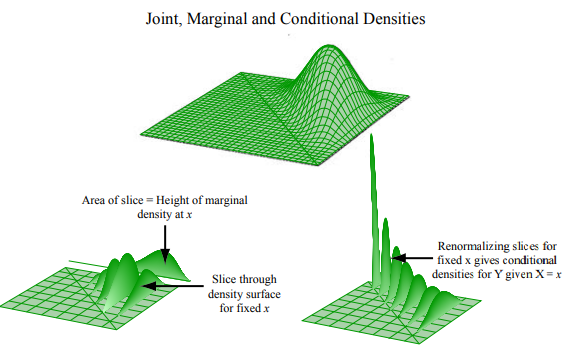
随机变量 \(X\) 和 \(Y\) 的联合 PDF、期望、边缘 PDF 和条件 PDF 如下,联合 PDF 表示的曲顶柱体的体积就是概率,在整个曲面下的体积 \(\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f_{X, Y} = 1\),密度 \(f_{X, Y} \geq 0\)。将前提 \(y\) 视为常量,条件 PDF 可以看作联合 PDF 的切片。
$$
P((X, Y) \in S) = \int\int_{S}f_{X, Y}(x, y)dxdy,\
P(x \leq X \leq x + \delta, y \leq Y \leq y + \delta) \approx f_{X, Y}(x, y) \cdot \delta^{2}
$$
$$
E[g(X, Y)] = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(x, y)f_{X, Y}(x, y)dxdy
$$
$$
f_{X}(x) \cdot \delta \approx P(x \leq X \leq x + \delta)
= \int_{-\infty}^{\infty}\int_{x}^{x + \delta}f_{X, Y}(x, y)dxdy
\approx \int_{-\infty}^{\infty}\delta \cdot f_{X, Y}(x, y)dy \rightarrow
f_{X}(x) = \int_{-\infty}^{\infty}f_{X, Y}(x, y)dy
$$
$$
f_{X \mid Y}(x \mid y) = \frac{f_{X, Y}(x, y)}{f_{Y}(y)} \quad (f_{Y}(y) \gt 0)
$$
$$
f_{X, Y}(x, y) = f_{X}(x)f_{Y}(y),\
f_{X \mid Y}(x \mid y) = f_{X}(x) \quad (X, Y \text{ are independent})
$$
Buffon’s needle 问题:有两条距离为 \(d\) 的平行线,以及长度为 \(l\) 的针(\(l \lt d\)),求针和直线相交的概率。取随机变量 \(X\) 表示针的中点到两条平行线的最短距离,随机变量 \(\Theta\) 表示针和直线的夹角(锐角)。假设 \(X\) 和 \(\Theta\) 服从均匀分布且相互独立,则联合 PDF 公式如下。由于针和直线在 \(X \leq \frac{l}{2}\sin\Theta\) 时相交,所以相交的概率为 \(P(X \leq \frac{l}{2}\sin\Theta) = \frac{2l}{\pi d}\)。
$$
f_{X, \Theta}(x, \theta)
= f_{X}(x)f_{\Theta}(\theta)
= \frac{2}{d}\frac{2}{\pi}
\quad (0 \leq x \leq d / 2, 0 \leq \theta \leq \pi / 2)
$$
$$
P(X \leq \frac{l}{2}\sin\Theta)
= \int\int_{x \leq \frac{l}{2}\sin\theta}f_{X}(x)f_{\Theta}(\theta)dxd\theta
= \frac{4}{\pi d}\int_{0}^{\pi / 2}\int_{0}^{(l /2)\sin\theta}dxd\theta
= \frac{2l}{\pi d}
$$
Lecture 10: Continuous Bayes’ Rule; Derived Distributions
$$
p_{X \mid Y}(x \mid y)
= \frac{p_{X, Y}(x, y)}{p_{Y}(y)}
= \frac{p_{X}(x)p_{Y \mid X}(y \mid x)}{p_{Y}(y)},\
p_{Y}(y) = \sum_{x}p_{X}(x)p_{Y \mid X}(y \mid x)
$$
$$
f_{X \mid Y}(x \mid y)
= \frac{f_{X, Y}(x, y)}{f_{Y}(y)}
= \frac{f_{X}(x)f_{Y \mid X}(y \mid x)}{f_{Y}(y)},\
f_{Y}(y) = \int_{x}f_{X}(x)f_{Y \mid X}(y \mid x)dx
$$
$$
p_{X \mid Y}(x \mid y)
= \frac{p_{X}(x)f_{Y \mid X}(y \mid x)}{f_{Y}(y)},\
f_{Y}(y) = \sum_{x}p_{X}(x)f_{Y \mid X}(y \mid x)
$$
$$
f_{X \mid Y}(x \mid y)
= \frac{f_{X}(x)p_{Y \mid X}(y \mid x)}{f_{Y}(y)},\
p_{Y}(y) = \int_{x}f_{X}(x)p_{Y \mid X}(y \mid x)dx
$$
对于离散型随机变量 \(X\),已知 \(X\) 的 PMF,则 \(Y = g(X)\) 的 PMF 如下。对于连续型随机变量 \(X\),已知 \(X\) 的 PDF,则 \(Y = g(X)\) 的 PDF 如下。可以使用以下公式证明,正态随机变量的线性函数仍服从正态分布。
$$
p_{Y}(y) = P(g(X) = y) = \sum_{x: g(x) = y}p_{X}(x)
$$
$$
F_{Y}(y) = P(Y \leq y),\
f_{Y}(y) = \frac{dF_{Y}}{dy}(y) \rightarrow
Y = aX + b,\
f_{Y}(y) = \frac{1}{|a|}f_{X}(\frac{y - b}{a})
$$
Lecture 11: Derived Distributions; Convolution; Covariance and Correlation
如果 \(Y = g(X)\) 且函数 \(g\) 严格单调递增,则随机变量 \(X\) 和 \(Y\) 的 PMF 满足以下关系。如果 \(W = X + Y\) 且 \(X\) 和 \(Y\) 独立,则有如下卷积公式 \(p_{W}(w)\) 和 \(f_{W}(w)\),分别对应离散和连续情况。可以使用卷积公式证明,独立的正态随机变量之和仍服从正态分布。
$$
P(\ x \leq X \leq x + \delta) = P(g(x) \leq Y \leq g(x + \delta) \approx g(x) + \delta|\frac{dg}{dx}(x)|) \rightarrow
\delta f_{X}(x) = \delta \left|\frac{dg}{dx}(x)\right|f_{Y}(y)
$$
$$
p_{W}(w) = \sum_{x}P_{X}(x)p_{Y}(w - x),\
f_{W}(w) = \int_{-\infty}^{\infty}f_{X}(x)f_{Y}(w - x)
$$
协方差大于零说明 \(X\) 和 \(Y\) 成正相关,小于零说明成负相关。如果 \(X\) 和 \(Y\) 独立,则协方差为零,反之不一定成立。类似方差和标准差,为消除单位的影响,提出相关系数 \(\rho\) 的概念,表示变量之间的关联程度。
$$
\DeclareMathOperator{\cov}{cov}
\cov(X, Y) = E\left[(X - E[X]) \cdot (Y - E[Y])\right]
$$
$$
\DeclareMathOperator{\var}{var}
\DeclareMathOperator{\cov}{cov}
\cov(X, X) = \var(X),\
\cov(X, Y) = E[XY] - E[X]E[Y],\
\var\left(\sum_{i = 1}^{n}X_{i}\right) = \sum_{i = 1}^{n}\var(X_{i}) + \sum_{(i, j): i \neq j}\cov(X_{i}, X_{j})
$$
$$
\DeclareMathOperator{\cov}{cov}
\rho = \frac{\cov(X, Y)}{\sigma_{X}\sigma_{Y}},\
-1 \leq \rho \leq 1
$$
$$
|\rho| = 1 \iff (X - E[X]) = c(Y - E[Y])
$$
Lecture 12: Iterated Expectations; Sum of a Random Number of Random Variables
$$
\DeclareMathOperator{\var}{var}
E[E[X \mid Y]] = \sum_{y}E[X \mid Y = y]p_{Y}(y) = E[X],\
\var(X) = E[\var(X \mid Y)] + \var(E[X \mid Y])
$$
$$
\DeclareMathOperator{\var}{var}
Y = \sum_{i = 1}^{N}X_{i},\
E[Y] = E[E[Y \mid N]] = E[NE[X]] = E[N]E[X],\
\var(Y) = E[\var(Y \mid N)] + \var(E[Y \mid N]) = E[N]\var(X) + (E[X])^{2}\var(N)
$$
Unit IV: Laws Of Large Numbers And Inference
Lecture 19: Weak Law of Large Numbers
$$
E[X] = \sum_{x}xp_{X}(x)
\geq \sum_{x \geq a}xp_{X}(x)
\geq \sum_{x \geq a}ap_{X}(x)
= aP(X \geq a) \quad (X \geq 0)
$$
$$
\DeclareMathOperator{\var}{var}
\mu = E[X],\
\var(X) = E[(X - \mu)^{2}]
\geq a^{2}P((X - \mu)^{2} \geq a^{2})
= a^{2}P(|X - \mu| \geq a)
$$
$$
\sigma^{2} = \int(x - \mu)^{2}f_{X}(x)dx
\geq \int_{-\infty}^{-c}(x - \mu)^{2}f_{X}(x)dx + \int_{c}^{\infty}(x - \mu)^{2}f_{X}(x)dx
\geq c^{2}P(|X - \mu| \geq c)
\rightarrow
P(|X - \mu| \geq c) \leq \frac{\sigma^{2}}{c^{2}}
$$
弱大数定律:如果 \(X_{i}\) 独立同分布,且 \(E[X_{i}] = \mu\)、\(\var(X_{i}) = \sigma^{2}\),则样本均值 \(M_{n}\) 依概率收敛到 \(\mu\)。中心极限定理:标准化 \(S_{n}\) 得到期望为 \(0\) 方差为 \(1\) 的随机变量 \(Z_{n}\),假设 \(Z\) 是标准正态随机变量,则 \(P(Z_{n} \leq c) \to P(Z \leq c)\) 对所有 \(c\) 都成立,即 \(Z_{n}\) 依分布收敛到 \(Z\)。由于 \(S_{n}\) 可以看作是 \(Z_{n}\) 的线性函数,且正态随机变量的线性函数仍服从正态分布,所以 \(S_{n}\) 近似服从正态分布。
$$
\DeclareMathOperator{\var}{var}
M_{n} = \frac{\sum_{i = 1}^{n}X_{i}}{n} \rightarrow
E[M_{n}] = \mu,\
\var(M_{n}) = \frac{\sigma^{2}}{n} \rightarrow
P(|M_{n} - \mu| \geq \epsilon) \leq \frac{\var(M_{n})}{\epsilon^{2}} = \frac{\sigma^{2}}{n\epsilon^{2}}
$$
$$
S_{n} = \sum_{i = 1}^{n}X_{n},\
Z_{n} = \frac{S_{n} - E[S_{n}]}{\sigma_{S_{n}}} = \frac{S_{n} - nE[X]}{\sqrt{n}\sigma}
$$
Lecture 21: Bayesian Statistical Inference - I



