阅读论文 GFS,参考 FAQ,note。
概念
GFS 是一个分布式文件系统,用于大型分布式数据密集型应用程序,例如 MapReduce。系统的设计基于以下场景:
- 系统由许多机器组成,所以会频繁发生故障。
- GB 级别的文件很多,普通文件系统会将文件划分为很多块,不便管理。
- 读负载由大量顺序读和少量随机读组成,写负载由大量追加写和少量随机写组成。
- 高持续带宽比低延迟更重要,应用程序需要快速进行批处理,而对响应时间没有严格要求。
实现
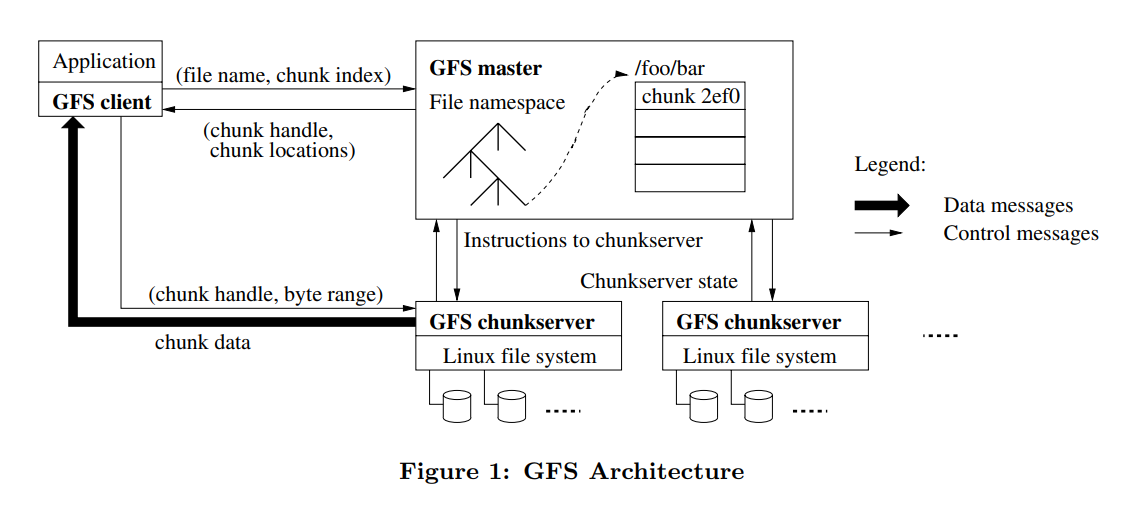
GFS 集群由单个 master 和多个 chunkserver 组成,由多个客户端访问。文件被划分为 64 MB 的块(chunk),每个块都是 chunkserver 中的一个文件。在分配空间时使用懒分配策略,避免产生内部碎片从而浪费空间。master 在创建块时,会为其分配一个不可变且全局唯一的 64 位块句柄(chunk handle)。每个块都会被复制到多个 chunkserver 上(默认三个),以保证系统的可靠性。
master 主要负责维护系统的元数据、存储日志和检查点、租约管理以及控制垃圾收集、重新复制、负载均衡和快照创建。元数据包括命名空间、访问控制信息、从文件名到块句柄数组的映射,以及为每个块维护版本号和副本所在 chunkserver 的列表。master 通过心跳消息定期与 chunkserver 通信,向其发出指令和收集其状态。chunkserver 主要负责存储文件数据、版本号和校验和,64 MB 的 chunk 被划分为 64 KB 的 block,每个 block 都有一个 32 位的校验和。
链接到应用程序的 GFS 客户端代码实现文件系统 API,通过与 master 和 chunkserver 通信来代表应用程序读写数据。客户端从 master 获取元数据,从 chunkserver 获取文件数据。客户端不需要缓存文件数据(但会缓存元数据),因为负载通常是顺序读和追加写。客户端没有实现 POSIX API,因此不需要挂钩到 Linux vnode 层。PS:我没有查到 Linux vnode 相关的资料,vnode 似乎是 BSD 中的概念,和 VFS 有关。
块大小
Linux 文件系统的默认块大小为 4 KB,GFS 使用 64 MB 的块大小是基于其 GB 级文件场景而设计的,优势如下:
- 由于应用程序通常是顺序读写文件数据,所以 64 MB 的块大小可以减少客户端和 master 的交互次数。
- 许多操作会发生在同一个块中,使得客户端和 chunkserver 保持长 TCP 连接,有利于减少网络开销。
- master 中的元数据更少,从而可以全部放入内存,避免磁盘 I/O。
同时,论文提到小文件可能只有一个块,面对多个应用程序的访问,存储该块的 chunkserver 有可能成为热点。GFS 的解决方案是使用更高的复制因子存储小文件,同时使批处理队列系统错开应用程序访问小文件的时间。潜在的解决方案是允许客户端在该情况下从其他客户端读取数据。
元数据
命名空间和映射会以操作日志(operation log)的形式持久化到 master 的本地磁盘和复制到远程机器,保证 master 能够在崩溃之后恢复。为保证一致性,只有在本地和远程将相应的日志刷新到磁盘之后,master 才会响应客户端的操作。可以对刷新和复制批处理,从而减少开销。当日志超过一定大小时,会创建检查点(使用 B 树),从而避免崩溃恢复时重放所有日志。由于创建检查点比较耗时,master 会切换到新的日志文件,并在单独的线程中创建检查点,以避免在创建检查点时停止执行(写)操作。检查点同样也会被复制到远程机器。
master 不会持久化块的位置列表,而是在启动时以及 chunkserver 加入集群时,向 chunkserver 询问其包含的块。因为块是否存在于某个 chunkserver 是由该 chunkserver 决定的,所以在 master 中持久化该信息没有任何意义,反而会面临同步问题。PS:说明 master 内存中的位置列表可能因为 chunkserver 故障,从而产生不一致。
命名空间其实就是一个将目录名和文件名作为节点的树,通过使用读写锁保证写操作的正确性。具体来说,读/写操作会获取路径上所有祖先节点的读锁,以及目标节点的读/写锁。锁在层级间按照自顶向下的顺序获取,在层级内按照字典序获取,从而避免死锁。PS:这让我想到 B+ 树的蟹行协议只锁定会被修改的节点,大概是因为 B+ 树的数据和路径不像文件和路径那样具有很强的关联性。
读操作
客户端使用固定的块大小,将应用程序指定的文件名和字节偏移量转换为文件内的块索引。然后,它向 master 发送包含文件名和块索引的请求,master 回复相应的块句柄(handle)、副本的位置列表,客户端使用文件名和块索引作为键来缓存该信息(会有过期时间)。
然后,客户端选择其中一个副本发送请求(很可能是距离最近的副本),该请求指定块句柄和块内字节范围。在缓存信息过期或重新打开文件之前,客户端不需要和 master 进行交互。客户端可以在向 master 发送的一个请求中请求多个块,master 也可以在回复中包含请求块之后的多个块信息(利用空间局部性),从而减少客户端和 master 交互的次数。
写操作
在发生写操作时,需要保证多个副本之间的一致性。GFS 使用租约(lease)实现一致性(租约是按块授予的),持有租约的 chunkserver 被称为 primary,其他包含副本的 chunkserver 被称为 secondary。租约的超时时间为 60 秒,primary 可以根据需要续约,续约请求包含在定期的心跳消息中发送给 master,master 也可以在租约到期之前撤销租约(用于快照创建)。如果 master 和 primary 发生网络分区故障,master 可以在旧租约到期之后向另一个副本授予租约,从而避免脑裂。
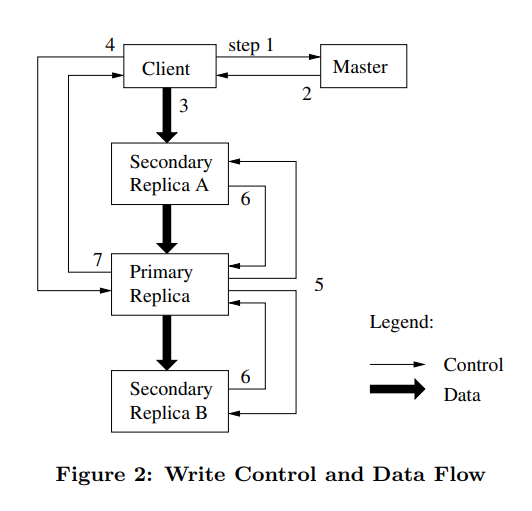
写操作的流程如下:
- 客户端首先向 master 询问 primary 和 secondary 的位置并将其缓存。如果 primary 不存在,则 master 任选一个包含副本的 chunkserver 授予租约。客户端会缓存位置信息,当 primary 不可达或者回复其租约过期时,客户端会重新联系 master。然后,客户端以流水线的方式将数据发送到 primary 和 secondary(存储在缓冲区中),并且等待它们的确认响应。
- 客户端收到所有副本的确认之后,向 primary 发送写请求,该请求会使用之前发送的数据。primary 为其收到的来自多个客户端的请求分配序列号(单个客户端的请求肯定是同步的,在收到响应之前不会发送第二个请求,因为 GFS 没法保证客户端请求的 FIFO 顺序),只有当 primary 本地执行成功之后,才会转发给所有 secondary,请求在所有副本上都按照序列号的顺序执行。当 primary 收到所有 secondary 的完成响应时,primary 回复客户端完成。
- 论文提到,副本的任何错误都会被报告给客户端,客户端会首先从步骤三开始重试几次,然后从步骤一开始重试。论文有一个前后矛盾的点,首先提到 primary 分配序列号然后应用到本地,之后又说如果在 primary 执行失败就不会分配序列号和转发。不过无关紧要。
一致性模型
GFS 具有宽松的一致性模型,数据突变之后文件区域的状态,取决于突变的类型(随机写和追加写)以及是否存在并发,如下图所示。如果无论客户端从哪个副本读取,始终看到相同的数据,则文件区域是一致的。如果文件区域一致,且客户端将会看到整个突变的内容,则文件区域是定义的。PS:这里的一致并不是严格一致性(可线性化)。
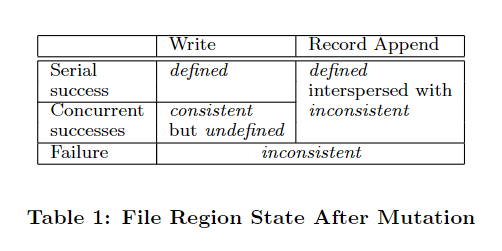
随机写:顺序突变成功状态是定义的和一致的;并发突变成功状态是一致的但是未定义,因为 GFS 使用租约保证突变以相同的顺序应用到所有副本(一致的),但是突变没有对文件区域加锁(未定义)。
追加写:不论是顺序还是并发突变成功,状态都是定义的,因为追加是原子操作且按照指定顺序应用到所有副本。只要有一个副本追加失败,客户端会重试整个追加操作,使得在未失败的机器上多次追加相同的数据,在失败的机器上填充无效的数据(因为追加会指定偏移量),从而产生不一致。特别的,追加的偏移量由 primary 指定,而不是单纯的追加到文件末尾,这可以保证多个副本在成功执行追加的偏移位置的数据是一致的,即使之前发生过失败。也就是说,中间区域不一致,最后区域一致。
此外,失败的突变总是会导致不一致。即使突变成功,数据最终一致,客户端仍可能观察到不一致,因为数据可以从任何包含副本的 chunkserver 读取。假设突变由客户端 A 发起,首先应用到 primary,再发送到 secondary。客户端 B 和 C 在突变过程中分别读取 primary 和 secondary,可以观察到不一致的情况。如果突变很慢,由于网络延迟或故障重试,单个客户端也可以观察到不一致。应用程序需要自行适应 GFS 的宽松一致性模型。
版本检测
如果 chunkserver 发生故障,从而错过突变,其上的块副本将会过时。master 和 chunkserver 会为块维护一个版本号,以此来区分新副本和旧副本。当 master 授予某个块租约时,它会递增该块的版本号,同时和 chunkserver 通信来递增最新副本的版本号。任何包含旧副本的 chunkserver 都不会返回给客户端,master 会在心跳检测中检查副本的版本,然后 master 会指示 chunkserver 对旧副本垃圾收集。作为额外的保护措施,master 会在回复客户端请求或指示 chunkserver 复制时包含版本号,客户端和 chunkserver 会在执行操作时进行验证。
故障处理
master 故障
当 master 发生故障时,GFS 的外部监控基础设施会使用检查点和日志快速恢复,即使磁盘发生故障也可以在其他机器上使用检查点和日志的副本进行恢复。客户端仅使用 DNS 别名访问 master(CNAME),其映射可以随时更改,以适应 master 机器的变更。此外,GFS 使用 shadow master 在 master 故障时提供对文件系统的只读访问,shadow master 略微滞后于 master。由于它存储的是元数据,文件数据存储在 chunkserver 中,所以客户端实际上不会读取到旧数据。
PS:论文提到 shadow master 会按顺序执行操作日志的副本,似乎 master 和 shadow master 的关系就是主从复制,但是为什么 shadow master 只提供只读访问,即使在 master 故障之后。它和 master 应该是最终一致的,为什么论文没有说 shadow master 在执行完所有日志之后会被提升为 master,虽然可以肯定需要人工操作,以避免原 master 只是网络分区故障,从而导致脑裂。
chunkserver 故障
master 使用心跳消息判断 chunkserver 是否存活,如果 master 判断 chunkserver 故障,它会指示其他 chunkserver 对不满足复制因子的数据块重新复制。当故障的 chunkserver 上线时,master 也会删除多余的副本,以及因错过突变而过时的副本。
其他功能
使用写时复制实现快照功能;跨机架的块放置策略;根据服务器的负载进行块放置和块迁移;根据优先级重新复制块以恢复冗余;延迟删除和垃圾收集;使用校验和检测数据块是否损坏;生成诊断日志(包含 chunkserver 的启动/关闭,RPC 的请求/回复记录,不包括文件数据)。
问题
Q:租约具体是如何工作的,master 和 chunkserver 如何判断租约是否过期?如何撤销租约?
A:论文没有说明,我猜测:master 首先发送授予租约的请求,chunkserver 收到请求之后开始计时,同时发送响应给 master,master 收到响应之后开始计时。这样 chunkserver 和 master 都可以判断租约是否到期,以及 master 的计时总是晚于 chunkserver,可以保证避免脑裂。撤销租约只修改 master 本地元数据肯定是不行的,因为客户端可能正在和持有租约的 chunkserver 通信,master 必须直接向 primary 发送撤销请求。
Q:根据上述猜测,如果授予租约的响应丢失,master 该如何处理?是否需要考虑时钟同步问题?
A:如果 master 没有收到响应,它就不会把该 chunkserver 记作 primary 返回给客户端,那么该租约实际上是一个无效租约,master 可以重试或者另选一个包含副本的 chunkserver。计算超时使用的是单调时钟,不需要同步。也可以使用时间戳判断租约是否到期,但是使用的是墙上时钟,需要服务器之间时钟同步。
总结
GFS 使用复制进行容错,从而引入多个副本间的一致性问题。但是仅保证宽松的一致性,而将问题交由应用程序处理,该设计基于其特殊的使用场景,顺序读写以及用于批处理,似乎强一致性显得不是很重要。可以查看课程的笔记和问答加深对论文的理解,笔记结尾的优缺点总结还是很不错的,有一个全局的视角,我有点过于关注一致性了。更多关于 GFS 的讨论,可以阅读 GFS: Evolution on Fast-forward。