幻灯片和笔记 ,其他同学整理的笔记 ,Discord 讨论 ,dbdb.io 。
本来想做个课程总结和项目总结的,但是有点没心情做,排行榜优化也暂时搁置吧。:(
更新:还是做一下总结,课程的内容不只下面这些,有很多内容对我来说可能用不到,所以没有记录。
Advanced SQL
查询满足某个条件的记录数量:
1 2 SELECT COUNT(*) FROM t WHERE xx; SELECT SUM(IF(xx, 1, 0)) FROM t;
查询满足某个条件的记录百分率:
1 SELECT ROUND(AVG(IFNULL(xx, 0)), 2) FROM t;
窗口函数(文档:12.20 Window Functions ):
1 2 SELECT ROW_NUMBER() OVER(PARTITION BY xx ORDER BY xx) FROM t; SELECT AVG(xx) OVER (PARTITION BY xx ORDER BY xx ROWS BETWEEN 1 PRECEDING AND 1 FOLLOWING)
日期和时间函数(文档:12.7 Date and Time Functions ):
1 2 SELECT DATE_FORMAT(xx, xx); SELECT DATEDIFF(xx, xx);
Database Storage
课程主要介绍面向磁盘的 DBMS,数据库以文件的形式存储在磁盘上,文件以特定于 DBMS 的方式编码,它被表示为页面的集合,每个页面都会有一个唯一标识符(页面 ID),大多数 DBMS 使用哈希表将页面 ID 映射为文件路径和文件内的偏移量。注意区分硬件页面(通常为 4 KB)、操作系统页面(4 KB)和数据库页面(1-16 KB)。存储设备可以保证硬件页面的原子写入,如果数据库页面大于硬件页面,则 DBMS 需要采取额外的措施来保证原子性。
每个页面被分为两部分:页面头部和页面内容。页面头部用于记录有关页面内容的元数据,包括页面大小、校验和、DBMS 版本、事务可见性和自包含(Self-containment)等。页面内容有两种主要的数据布局方式:slotted-pages 和 log-structured。
Storage Models & Compression
三种工作负载:OLTP(在线事务处理),OLAP(在线分析处理),HTAP(混合事务和分析处理)。
两种存储模型:行式存储和列式存储。
Memory Management
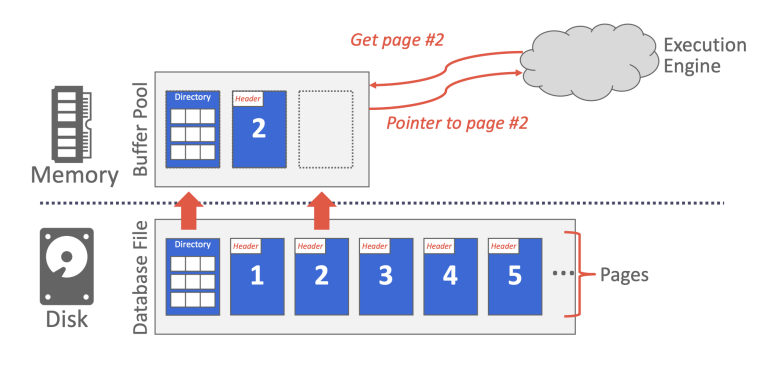
缓冲池实际上是一个页面数组,用于缓存磁盘中的页面,为了区分缓冲池页面和磁盘页面,我们将缓冲池页面称为帧(frame)。当 DBMS 请求一个页面时,存储管理器会首先搜索缓冲池,如果页面不在缓冲池中,就将该页面从磁盘复制到空闲的帧中。(有关缓冲池的详细信息可以参考 Project #1)
缓冲池优化方式:
多缓冲池:可以为不同数据库或不同页面类型提供不同的缓冲池,这样可以根据其中的数据定制优化策略。
预取:可以根据查询计划预取页面,通常在顺序访问页面时进行该优化。
扫描共享(同步扫描):当多个查询扫描的数据存储重叠时,重叠部分可以只进行一次扫描。
缓冲池绕过:顺序扫描或临时数据处理不会将页面存储在缓冲池中,而是为其单独开一块内存,以避免缓冲池污染,因为这些页面通常不会再被访问。
大部分数据库使用直接 I/O 绕过操作系统缓存,以避免多余的页面缓存(Postgres 除外)。
Hash Tables
哈希表的实现由两部分组成:
哈希函数:需要在计算速度和冲突率之间进行权衡。
哈希模式:发生冲突时如何处理。(静态哈希和动态哈希)
Trees Indexes
索引的数量越多,查询的速度就越快,但是索引占用的存储空间以及维护成本也会随之提高。
B+ 树是一种平衡查找树,它保持数据有序,并且支持 \(O(\log{n})\) 的查询、插入和删除操作。B+ 树平衡的关键在于,它要求所有节点都至少是半满的。B 树在所有节点中存储值,而 B+ 树只在叶子节点中存储值。B+ 树相比哈希表的优势在于可以进行范围查询以及模糊查询。(有关 B+ 树的详细信息可以参考 Project #2)
Index Concurrency Control
区分 Lock 和 Latch:
Lock:高级原语,作用是保护数据库的内容(元组、表和数据库),在事务中使用。
Latch:低级原语,作用是保护数据库的内部数据结构,在临界区中使用。
实现 Latch 的底层原语是比较并交换(CAS)原子指令。有多种不同类型的 Latch 可供 DBMS 使用:
Blocking OS Mutex:使用操作系统内置的互斥锁基础设施,Linux 提供 futex(fast user-space mutex),它由用户空间的自旋锁和操作系统级别的互斥锁组成。示例 std::mutex,优点是使用简单,缺点是加锁/解锁的时间成本较高并且不可扩展(如果发生竞争,则当前线程会被操作系统阻塞)。
Test-and-Set Spin Latch(TAS):自旋锁具有更高的灵活性,DBMS 可以控制当存在竞争时应该执行什么操作。示例 std::atomic<T>,优点是加锁/解锁更快,缺点是在竞争比较激烈时,会浪费很多 CPU 资源。
Reader-Writer Latches:示例 std::shared_mutex,优点是可以并发读取,缺点是需要额外的空间存储读/写队列。
B+ 树使用蟹行协议(Latch Crabbing Protocol)来保证自上而下的加锁顺序,当线程的访问模式不包含叶节点扫描时,该实现方式可以避免死锁。因为索引锁不支持死锁检测或避免(疑问:这里的描述和幻灯片 第 23 页的内容不太一样),所以叶节点扫描在获取同级锁时遵循无等待模式,即如果获取同级锁失败就立即重启操作。
Sorting & Aggregations Algorithms
排序可能被用在 ORDER BY、GROUP BY、JOIN 和 DISTINCT 操作中。如果数据能够放入内存,则可以使用快速排序(当查询包含 LIMIT 和 ORDER BY 时,可以使用堆排序),否则使用外部归并排序。
外部归并排序由两部分组成:
排序:将数据分为多个可以放入内存的数据块,分别进行排序,然后将排序后的数据写回磁盘。
合并:将排序后的数据块合并。
外部归并排序的 I/O 成本分析:
假设 \(N\) 为数据页面的个数,\(B\) 为可以使用的缓冲区页面的个数。
在排序阶段,每次可以读取 \(B\) 个数据页面到缓冲区,进行排序之后写回磁盘,总共执行 \(\lceil \frac{N}{B}\rceil\) 次排序,I/O 成本为 \(2N\)(读入缓冲区和写回磁盘各一次)。
在合并阶段,可以使用 \(B-1\) 个缓冲区页面存储 \(B-1\) 个数据块的第一个页面,剩下一个缓冲区页面存储合并的结果并根据需要写回磁盘,如果将合并的过程看作多叉树,则树的高度为 \(\lceil\log_{B-1}{\lceil \frac{N}{B}\rceil}\rceil\),每层合并都会将所有数据读写一次,I/O 成本为 \(2N\times\lceil\log_{B-1}{\lceil \frac{N}{B}\rceil}\rceil\)。
最后,总 I/O 成本为 \(2N\times(1+\lceil\log_{B-1}{\lceil \frac{N}{B}\rceil}\rceil)\)。
外部归并排序可以使用双缓冲区优化,前台缓冲区进行计算的同时,后台缓冲区预取数据。如果数据在排序键上存在 B+ 树聚集索引,那么可以直接遍历索引得到有序数据。因为,如果是聚集索引,数据访问将是顺序 I/O,成本为 \(N\);如果是非聚集索引,数据访问将是随机 I/O,成本为 \(N\times M\),其中 \(M\) 为每页中的记录个数(缓冲区大小有限,随机 I/O 会导致页面抖动)。
聚合操作有两种实现方式:
排序:首先将数据按照聚合键进行排序,然后对有序数据执行顺序扫描来计算聚合值。
哈希:除非数据已经有序,否则哈希总是比排序更高效。由于内存可能容纳不下整个哈希表,为了避免随机 I/O,肯定不能将哈希表直接溢出到磁盘。我们可以首先进行一次哈希,将数据分区,然后对每个分区单独进行聚合操作,这样每个分区的哈希表大小应该会足够小,最好情况是能放入内存中。
Joins Algorithms
连接操作有两种输出模式:
提前物化(early materialization):将外表和内表的所有属性都放入临时表。
延迟物化(late materialization):只将连接键以及外表和内表的记录 ID 放入临时表。
连接算法的 I/O 成本分析(假设连接是等值连接):
假设外表 \(R\) 有 \(M\) 页,总共包含 \(m\) 个元组;内表 \(S\) 有 \(N\) 页,总共包含 \(n\) 个元组。
Nested Loop Join:
该算法由两个嵌套的 for 循环组成,外层循环遍历外表,内层循环遍历内表,如果两个元组满足连接谓词,则将它们连接并输出。注意,我们总是应该使用较小的表作为外表,因为。
Naive Nested Loop Join:对于外表的每个元组,将其和内表中的每个元组进行比较,I/O 成本为 \(M+(m\times N)\)。
Block Nested Loop Join:对于外表的每个块,将其和内表中的每个元组进行比较。假设有 \(B\) 个可用的缓冲区,该算法可以使用 \(B-2\) 个缓冲区扫描外表,\(1\) 个缓冲区扫描内表,\(1\) 个缓冲区存储连接结果,I/O 成本为 \(M+(\lceil \frac{M}{B-2}\rceil\times N)\)。
Index Nested Loop Join:如果内表在连接键上建有索引(或者临时建立索引),那么可以直接使用索引搜索到满足条件的元组,I/O 成本为 \(M+(m\times C)\),其中 \(C\) 为单次索引搜索的成本。
Sort-Merge Join:
首先对外表和内表进行排序,然后使用双指针分别遍历外表和内表,来进行连接谓词判断。如果内表的连接键有重复值,那么内表指针在匹配时可能需要回退。当外表或内表已经有序,或者输出结果要求按照连接键排序时,可以选择使用该算法。
排序成本:外表为 \(2M\times(1+\lceil\log_{B-1}{\lceil \frac{M}{B}\rceil}\rceil)\),内表为 \(2N\times(1+\lceil\log_{B-1}{\lceil \frac{N}{B}\rceil}\rceil)\)。
合并成本:最坏情况下,两个表中的所有元组的连接键都相等,合并的成本为 \(MN\)。一般情况下,连接键大多是唯一的,合并成本为 \(M+N\)。
Hash Join:
Basic Hash Join:首先将外表的连接键作为 key 构建哈希表,将外表的元组或者元组 ID 作为 value。然后对于内表中的每个元组,可以直接通过哈希表获取匹配的元组。由于可能存在哈希冲突,即使元组被哈希到某个桶,在桶内肯定还需要进行比较来判断元组是否真的匹配,这里我们可以额外使用布隆过滤器来过滤元组,以减少磁盘 I/O。
Grace Hash Join / Partitioned Hash Join:当哈希表无法放入内存时,Basic Hash Join 存在页面抖动问题,解决该问题的方法是进行分区。首先分别对外表和内表构建哈希表,并根据需要写入磁盘,如果单个桶都无法放入内存,则递归的进行分区(前提是桶内的键存在不同,否则会导致无限递归),I/O 成本为 \(2\times(M+N)\)。然后将外表和内表对应的桶进行嵌套循环连接,此时页面都可以放入内存,I/O 成本为 \(M+N\)。
假设 \(M=10^{3}\),\(m=10^{5}\),\(N=5\times 10^{2}\),\(n=4\times 10^{4}\),\(B=100\),每页的 I/O 花费 \(0.1\) 毫秒,各个算法花费的时间如下:
Algorithm
I/O Cost
Example
Naive Nested Loop Join
\(M+(m\times N)\)
1.4 hours
Block Nested Loop Join
\(M+(M\times N)\)
50 seconds
Index Nested Loop Join
\(M+(m\times C)\)
Varies
Sort-Merge Join
\(M+N+(sort cost)\)
0.75 seconds
Hash Join
\(3\times(M+N)\)
0.45 seconds
该表是课程笔记上的,但是有点疑问,Block Nested Loop Join 的 I/O 成本计算公式有问题吧,如果按照之前说的公式计算,I/O 花费的时间是 \(0.65\) 秒。
Query Execution
DBMS 将 SQL 语句转化为查询计划,查询计划由操作符构成的树表示,数据从叶子节点流向根节点,根节点的输出就是查询的结果。处理模型(processing model)定义系统如何执行查询计划,下面介绍三种处理模型:
迭代器模型/火山模型(Iterator Model):每个操作符都会实现 Next 函数,该函数由其父节点调用,以获取子节点的输出元组。因为每次调用只会返回单个元组,所以 Next 函数的调用一般放在循环中。调用从根节点传递到叶子节点,数据从叶子节点通过层层处理返回至根节点(实际上就是一个递归的过程,有点像树的后序遍历)。该模型允许以流水线的方式处理元组,有些操作符需要其子节点传递所有元组才能进行计算,包括哈希连接、子查询和排序等,这些操作符被称为流水线破坏者(pipeline breakers)。
物化模型(Materialization Model):每个操作符都会实现 Output 函数,该函数会返回所有元组。该模型相比迭代器模型可以减少函数的调用次数,适合 OLTP 工作负载,因为其单词查询访问的数据量不大,而 OLAP 工作负载会查询大量数据,操作符的返回结果将会溢出到磁盘,从而增加 I/O 成本。
向量模型(Vectorization Model):类似迭代器模型,区别在于每次调用 Next 会返回一批元组(即向量)。该模型适合访问大量数据的 OLAP 工作负载,相比迭代器模型,它可以减少函数调用的次数,还可以允许使用 SIMD 指令成批的处理元组。
PS:这些模型实际上是很简单的东西,无非就是返回的数据量不同,写这么多是不是有点浪费笔墨,额。这让我想起之前的一个感想,有些术语看上去很难懂,但是它们的本质其实非常简单,所以有些东西真的是增加学习难度。如无必要,勿增实体,不知道放在这合不合适。
Query Planning & Optimization
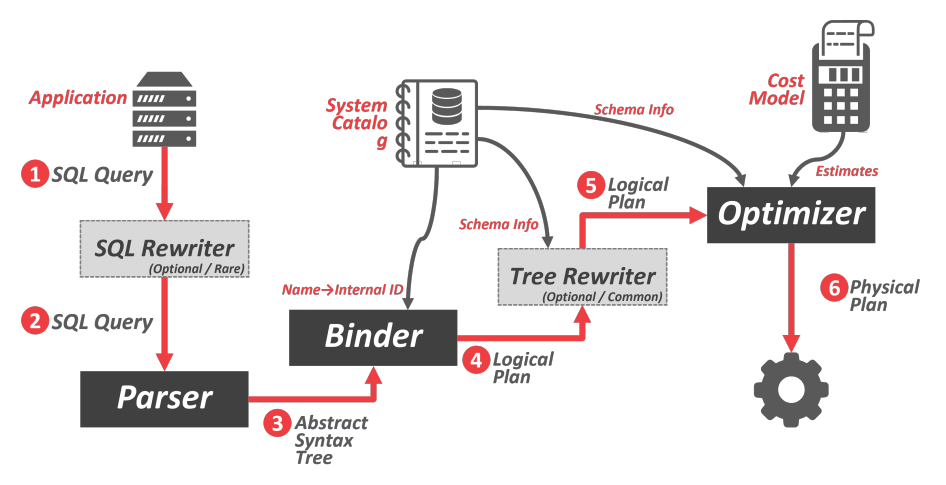
应用程序连接到数据库并发送 SQL 查询,该查询可以被重写为不同的形式,然后查询被解析为抽象语法树,绑定器通过查看系统目录,将语法树中的命名对象替换为内部标识,并生成逻辑计划,该逻辑计划同样可以被重写,之后优化器使用成本模型进行估计,将逻辑计划转化为物理计划。
逻辑计划和物理计划的区别:逻辑计划只描述了抽象的关系代数表达式,物理计划将抽象的表达式对应到某个具体实现,例如连接运算符有多种不同实现。逻辑计划和物理计划并不总是一一对应的。
查询优化有启发式优化(heuristics)和基于成本的搜索(cost-based search)两种策略:
启发式方法将查询的各个部分与已知的模式进行匹配,以将其转换为更有效的模式。
基于成本的搜索枚举等价的查询计划,然后选择成本最低的那个。
基于成本的搜索,如何估计谓词的选择性(就是谓词选择的数据占总数据的比率):
关系 \(R\) 中的元组数量 \(N_{R}\),属性 \(A\) 的不同值的数量 \(V(A,R)\)。使用这两个信息就可以计算出每个属性值的平均记录数 \(\frac{N_{R}}{V(A,R)}\),称作选择基数(selection cardinality)。DBMS 可以根据选择基数估计谓词的选择性。
由于数据并不是均匀分布的,各个谓词之间也不是相互独立的,所以通过选择基数估计谓词的选择性偏差较大。DBMS 还可以维护等宽/等深直方图,或者对原表进行抽样得到类似原表分布的副本表,然后通过遍历副本表来计算选择性。
Concurrency Control Theory
关键问题:如何避免竞态条件(race condition),以及实现崩溃恢复。
事务的 ACID 原则:
原子性:事务中的操作要么全部执行,要么都不执行。有两种实现方式:日志(主流实现),写时复制。
一致性:数据在逻辑上是正确的,遵循完整性约束。
隔离性:并发执行的事务相互隔离,就像在串行执行一样,通过使用并发控制协议(concurrency control protocol)实现。并发事务之间存在三种冲突:读写冲突(不可重复读),写读冲突(脏读),写写冲突(丢失修改)。
持久性:已提交的事务所做的修改将会持久化到磁盘上。
Two-Phase Locking Concurrency Control
两阶段锁(2PL)是一种悲观的并发控制协议,将事务执行过程分为两个阶段:加锁阶段(Growing)和解锁阶段(Shrinking)。两阶段锁存在脏读和死锁等问题,它有多个变体:
Conservative Two-Phase Locking(C2PL):在事务开始时获取需要的所有锁,此协议可以避免死锁。
Strict Two-Phase Locking(S2PL):事务结束时释放写锁,读锁可以在解锁阶段逐步释放,此协议可以避免脏读。
Strong Strict Two-Phase Locking(SS2PL):事务结束时释放读/写锁,此协议在 S2PL 的基础上保证了事务的提交顺序(Commitment Ordering,CO)。
死锁是事务之间发生循环等待的现象,2PL 中有两种处理死锁的方法:
死锁检测:DBMS 定期构建等待图,如果图中存在环,则通过中止环中的某个事务,来打破循环。
死锁预防:当一个事务试图获取另一个事务持有的锁时,DBMS 会中止两个事务中的某个事务,从而避免死锁。
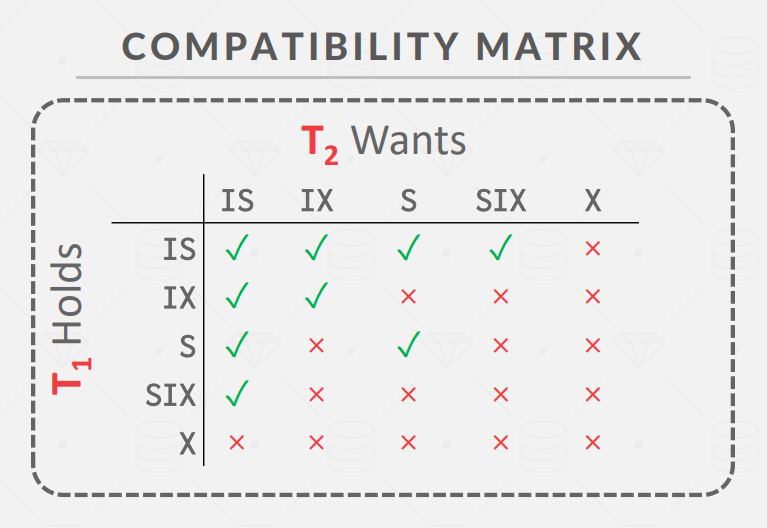
锁兼容矩阵图:
锁升级矩阵图:
持有锁
目标锁
IS
S,X,IX,SIX
S
X,SIX
IX
X,SIX
SIX
X
存在的异常:脏读、不可重复读和幻读。隔离级别:读未提交、读已提交、可重复读和可串行化。(基于 2PL 实现的隔离级别、死锁检测可以参考 Project #4)
Timestamp Ordering Concurrency Control
Timestamp Ordering(T/O)和 Optimistic Concurrency Control(OCC) 都是乐观的并发控制协议,这些协议假设事务之间很少发生冲突,并且使用时间戳而不是锁来控制事务的执行顺序。
Basic Timestamp Ordering(BASIC T/O):每个事务都会被分配唯一的时间戳,每个数据库对象都会记录最后一次被读/写的时间戳。每当事务读/写数据库对象时,都会将事务时间戳和对象时间戳做比较,以此确定操作是否能够执行。事务还需要保留对象的本地副本,以确保可重复读。
Optimistic Concurrency Control(OCC):该协议将数据库对象复制到本地进行更改(写时复制),当事务想要提交时,进行冲突检测(比较事务的时间戳),如果通过则将事务的本地更改应用到数据库。
PS:这节课有点没太明白,特别是 OCC 的验证阶段看不懂。
Multi-Version Concurrency Control
多版本并发控制(MVCC):DBMS 维护数据库中单个逻辑对象的多个物理版本,当事务开始时,DBMS 会创建数据库快照(通过复制事务状态表),然后根据快照来确定事务可见的对象版本。
MCC 有四个重要的设计决策:使用什么并发控制协议(2PL、T/O、OCC),多版本的存储方式,垃圾收集(回收对所有事务都不可见的版本),索引管理(辅助索引存储对象的逻辑指针还是物理指针,主键索引总是存储对象的物理指针)。
Database Logging
崩溃恢复算法的两个关键原语:
UNDO:回滚不完整的更改。
REDO:如果已提交事务的更改没有写入磁盘,则重做这些更改。
两个崩溃恢复算法:
写时复制:字面意思。该算法的 UNDO 操作就是删除所有页面副本,没有 REDO 操作,因为事务提交的同时会原子的修改数据库根节点的指针,即已提交的事务必定会将更改落实到数据库中。
预写日志(Write-Ahead Logging,WAL):日志首先存放在日志缓冲区中,DBMS 必须先将日志写入磁盘(顺序 I/O),然后才能将脏页写入磁盘(不需要立即执行,可以使用后台线程进行写入操作)。只有当日志写入磁盘,事务才能被视为已提交。DBMS 可以通过批量提交事务,来避免频繁的日志 I/O 操作。每个日志记录都包含:事务 ID,对象 ID,之前的值(用于 UNDO),之后的值(用于 REDO)。(这里应该是指物理日志)
日志的模式(Logging Schemes):
物理日志(Physical Logging):记录数据的字节级更改。
逻辑日志(Logical Logging):记录 INSERT、DELETE 和 UPDATE 语句。
混合日志(Physiological Logging):混合方法,以逻辑地址(页面中的槽号)的方式记录物理日志。
Database Recovery
Algorithms for Recovery and Isolation Exploiting Semantics(ARIES) 是由 IBM 在 1990 年代开发出的恢复算法,该算法包含三个关键概念:
Write Ahead Logging:先将日志写入磁盘,才能将脏页写入磁盘。
Repeating History During Redo:数据库重启时,重做日志将数据库恢复到崩溃之前的状态。
Logging Changes During Undo:将回滚操作记录到日志中,以确保再次崩溃时不会重复回滚。
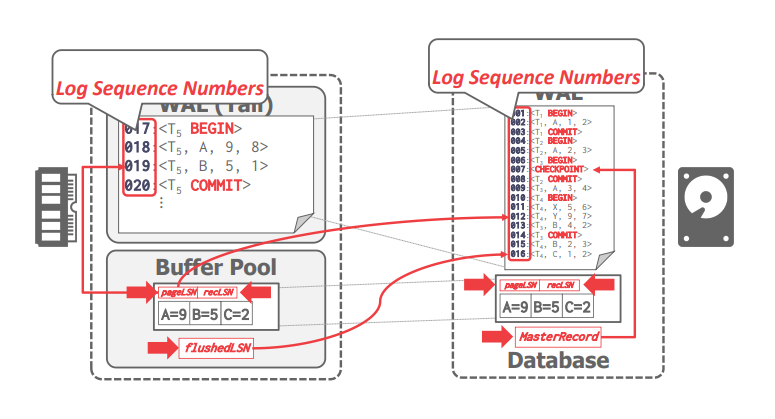
该算法为每个日志记录分配全局唯一的日志序列号(log sequence number,LSN),系统中的各个组件会跟踪与其相关的 LSN。每个数据页面会包含最近一次更新对应的 LSN(\(pageLSN\)),缓冲池会包含已经刷到磁盘的最大 LSN(\(flushedLSN\)),DBMS 在将第 \(i\) 页刷新到磁盘之前,必须保证 \(pageLSN_{i}\leq flushedLSN\),即预写日志。
事务提交:DBMS 首先将 COMMIT 日志记录写入日志缓冲区,然后将日志刷新到磁盘(顺序 I/O)。当日志已经成功刷新到磁盘之后,DBMS 就会向应用程序返回事务提交成功的信息。在之后的某个时刻,DBMS 将 TXN-END 日志记录写入日志缓冲区,表明该事务已经完成。(额,课程中没有说明在这段时间内,事务会执行什么操作)
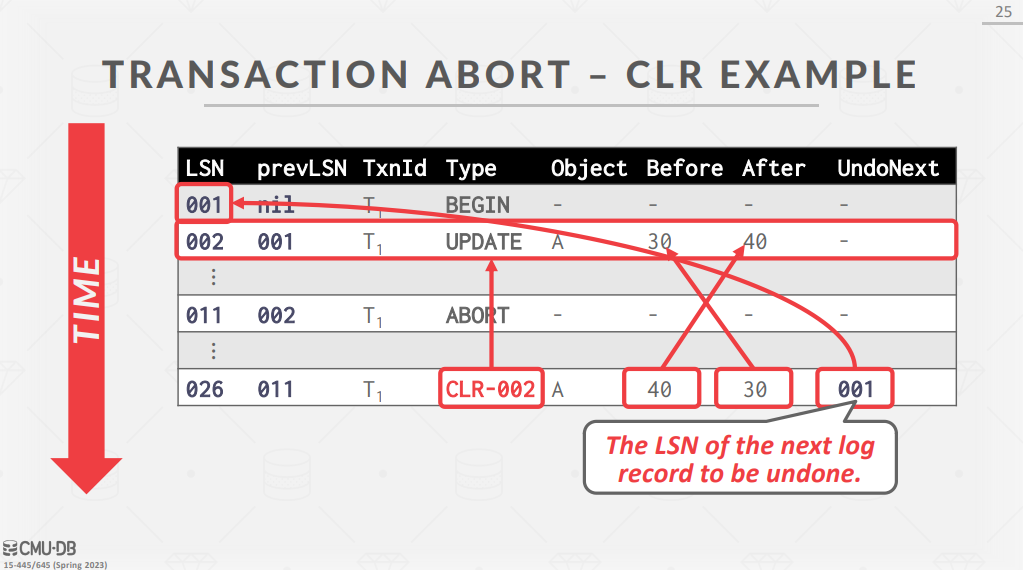
事务中止:每个日志记录会包含 \(prevLSN\) 字段,表示该 LSN 在事务中对应的上一个 LSN 是多少。DBMS 使用 \(prevLSN\) 维护事务的日志链表,以方便进行 UNDO 操作。这里引入一个新类型的日志 compensation log record(CLR),表示所执行的 UNDO 操作,该类型的日志不会被 UNDO。事务中止时,DBMS 首先将 ABORT 日志记录写入日志缓冲区,然后根据 ABORT 日志的 \(prevLSN\) 回滚事务的更新,当回滚完成时 DBMS 将 TXN-END 日志记录写入日志缓冲区。
为了避免数据库崩溃之后重做整个日志,DBMS 会定期设置检查点(Checkpoint,其实就是存档),在设置检查点时会将缓冲池中的所有脏页都刷新到磁盘中,Checkpoint 有下面几种实现方式:
Blocking Checkpoints:首先停止开始新事物,等待活动事务完成,然后将日志和脏页刷新到磁盘,最后将 CHECKPOINT 日志记录写入缓冲区并刷新到磁盘。之所以要停止并等待事务,是为了避免丢失更新。
Slightly Better Blocking Checkpoints:在开始设置检查点时,会记录内部系统的状态,从而不必等待活动事务完成,取而代之的是暂停活动事务。内部系统状态包括:Active Transaction Table(ATT)和 Dirty Page Table(DPT)。
Fuzzy Checkpoints:通过使用额外的日志记录(CHECKPOINT-BEGIN 和 CHECKPOINT-END)跟踪检查点的边界,从而不需要暂停活动事务。
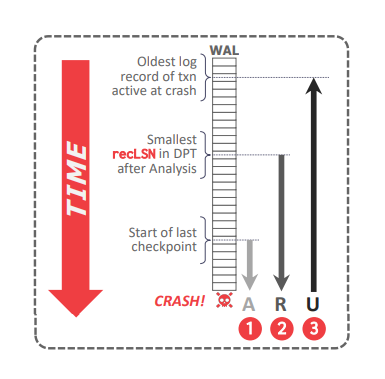
ARIES 算法在 DBMS 崩溃重启之后执行,分为三个阶段:
分析(Analysis):从 \(MasterRecord\) 对应检查点开始扫描日志,以构建 ATT 和 DPT,它们包含崩溃时缓冲池中存在的脏页以及活动的事务信息。
重做(Redo):从 DPT 的所有脏页中最小的 \(recLSN\) 开始重做,即所有脏页中最旧的修改日志记录。
回滚(Undo):从崩溃时所有活动事务中最旧的日志记录开始,撤销崩溃时活动事务所做的修改。
Introduction to Distributed Databases
并行数据库和分布式数据库的区别:
并行数据库
分布式数据库
节点之间距离较近
节点之间距离较远
节点之间使用高速局域网连接
节点之间使用公共网络连接
通信的成本很小且可靠
通信的成本很高且不可靠
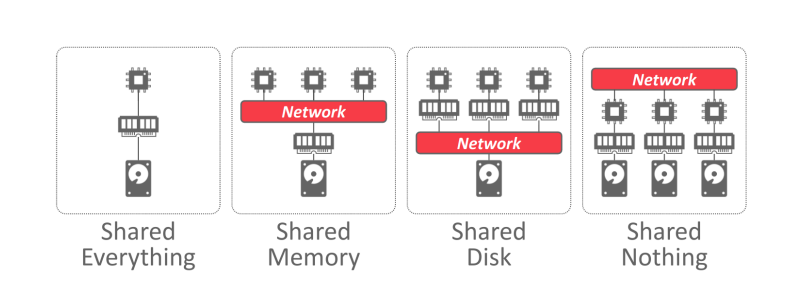
DBMS 的系统架构指定 CPU 可以访问哪些共享资源,有如下四种架构方式:
一致性哈希:
优势:假设有 \(n\) 个键,\(m\) 个节点,则一致性哈希平均只需要对 \(\frac{n}{m}\) 个键进行再散列。
原理:使用哈希函数将键和节点映射到圆上,每个键都会被分配给在顺时针方向上的下一个节点。每当添加一个节点时,只需要对其顺时针方向的下一个节点上的键进行再散列;每当删除一个节点时,只需要将当前节点的键移动到顺时针方向的下一个节点。(相当于多个节点将圆划分为多个圆弧,每个节点只包含映射到对应圆弧上的键)
Distributed OLTP Database Systems
如果某个事务需要访问多个节点上的数据(由于数据分区),则其是分布式事务。提交分布式事务时,根据协议的不同,可能需要得到所有或大多数节点的同意。原子提交协议(Atomic Commit Protocols)有:Two-Phase Commit,Three-Phase Commit,Paxos,Raft,ZAB,Viewstamped Replication。如果节点不可信,则需要使用拜占庭容错(byzantine fault tolerant)协议。
PS:虽然该课程将以上算法统称为原子提交协议,但是 2PC/3PC 和其他共识算法有一个显著的区别,就是 2PC/3PC 通常用于分布式事务,而其他共识算法通常用于数据复制。前者涉及多个节点上的不同数据,且协调器存在单点故障。后者涉及多个节点上的相同数据,且基于多数原则,不存在单点故障。可以将 2PC/3PC 和其他共识算法结合使用,从而消除单点故障(例如 Spanner 分布式数据库所做的)。
CAP 定理(Consistency,Availability,Partition tolerance):指在发生网络分区故障时,要么选择一致性(指的是可线性化),要么选择可用性(允许读写网络分区节点)。