参考 RateLimiter 代码。
基本使用
1 | <dependency> |
1 | RateLimiter rateLimiter = RateLimiter.create(1); |
代码实现
抽取 SmoothBursty 限流器的关键代码,梳理基本的实现流程。
1 | class RateLimiter { |
1 | // 当前时间大于 nextFreeTicket,生成 maxPermits 个许可 |
参考 RateLimiter 代码。
1 | <dependency> |
1 | RateLimiter rateLimiter = RateLimiter.create(1); |
抽取 SmoothBursty 限流器的关键代码,梳理基本的实现流程。
1 | class RateLimiter { |
1 | // 当前时间大于 nextFreeTicket,生成 maxPermits 个许可 |
CMU 15-445/645 — Fall 2024 Projects
参考 课程网站,项目地址,测试网站,Discord 频道。尝试做一下新版的项目。
HyperLogLog 主要用于近似计算 multiset 中的基数(不同元素的数量),相比精确计算需要的 \(O(n)\) 空间 \(n\) 为基数的大小),该算法只需要使用很少的内存。
基本想法是,使用哈希函数将多重集合的元素映射到均匀分布的随机数上,然后记录最左或者最右连续 \(0\) 的最大数量。利用哈希值的随机性,某个比特位为零的概率是 \(\frac{1}{2}\),如果最多 \(n\) 个连续的零,则估计多重集合的基数为 \(2^{n}\),因为该哈希值出现的概率是 \(\frac{1}{2^{n}}\)。
不过该算法方差较大,只要有一个哈希值包含很多零,就会严重高估基数。所以,可以将多重集合拆分为多个子集,通常是利用哈希值的前 \(k\) 个比特位确定元素拆分到的桶,然后每个桶内维护剩余比特位中连续零的最大值,取加权平均值 \(2^{\frac{1}{m}\sum_{i=1}^{m}{R_{i}}}\) 得到每个桶的平均基数(其中 \(m=2^{k}\)),然后再乘以 \(m\) 得到多重集合的基数估计值。
额外的优化是使用 constant=0.79402 和调和平均来提升准确率,使用稀疏布局和密集布局来平衡内存开销和准确率,最后计算公式如下。(参考 HyperLogLog in Presto: A significantly faster way to handle cardinality estimation,A problem so hard even Google relies on Random Chance,HyperLogLog)
① n_bits 的范围可以确定下限是 0,上限不确定,如果很大会内存溢出。② 很多地方使用的是无符号整数,在使用字面量时需要声明后缀(例如 1UL),以及做算术运算时需要避免溢出(例如取负值时需要转为有符号数)。③ 做移位操作 1 << x 时需要注意 x 的大小,如果结果超出表示范围则行为未定义。经过测试不同环境 1 << 32 会得到 0 或者 1。④ 可以使用 ./test/hyperloglog_test --gtest_filter=HyperLogLogTest.EdgeTest1 执行指定的测试。
简单的实现,使用单个哈希表维护 frame_id 到 LRUKNode 的映射关系,LRUKNode 负责维护该页面的最后 k 次访问时间戳,在淘汰时通过扫描整个哈希表来确定需要淘汰哪个 frame_id,淘汰的时间复杂度为 \(O(n)\)。如果使用两个链表分别维护 <k 和 >=k 的 Frame 访问顺序,如果不考虑 Pin,那么可以 \(O(1)\) 时间实现淘汰。但是由于不知道 Frame 是否被 Pin,所以仍然需要遍历链表查找第一个未被 Pin 的 Frame。也可以使用类似 TreeMap 的结构,直接存储未被 Pin 的所有 Frame,按照次数、时间戳排序,淘汰的时间复杂度是 \(O(\log{n})\),不过每次访问都需要重新删除插入来保证排序。(实际上都差不多,因为 BPM 的主要瓶颈在磁盘 I/O)
比较有意思的设计就是毒丸(poison pill),队列中存储的是 std::optional<bustub::DiskRequest> 类型的元素,向队列中添加 std::nullopt 元素,表示终止工作线程的执行。
缓冲池的基本功能就是获取 Frame,可以从空闲列表或者淘汰 Frame 来获取。如果是通过淘汰获取,则需要删除 Frame 和 Page 的映射关系、将脏页刷盘以及重置 FrameHeader。然后可以将 Frame 和 Page 关联,需要设置 Frame 和 Page 的映射关系、设置 FrameHeader 的成员变量、从磁盘读取数据、调用 LRUK 相关函数。
最后可以将该 Frame 和 PageGuard 关联,由于 PageGuard 会获取 Frame 的读写锁,所以要在创建 PageGuard 之前解锁 BPM 独占锁,从而避免 BPM 阻塞在 Frame 的锁上。例如,典型的情况是有两个线程同时对相同的 Page 获取 WritePageGuard。
线上测试就只有 BufferPoolManagerTest.SchedulerTest (0/0) 没有过,花几个小时找 BUG 都没找到,最后还是简单暴力打印日志解决问题。只能说别想太多,问题出在 is_dirty_ 的设置位置不对,我在 GetDataMut 方法中设置,而即使不调用该方法,NewPage 得到的空白页面也算是脏页,所以要在构造函数中设置。而且,调用 FlushPage/FlushAllPages 之后不应该将脏页标志重置,因为只要 WritePageGuard 还在那么页面依然可能变脏。(如果在刷盘的过程中修改页面,或许会产生问题,应该在刷盘之前获取 Frame 的读写锁,但是要避免和 BPM 独占锁产生死锁,这个点暂时不做)
简单的想法是在磁盘 I/O 时不持有 BPM 锁,而是直接解锁然后在磁盘 I/O 结束之后加锁。但是在如下交错下,相同的页面会占用多个 Frame(Problem #1)。解决方式也有,就是在解锁 BPM 之前更新 Page 和 Frame 之间的映射关系。但是会有新的并发问题,也就是之后的线程判断 Page 在缓冲池中,然后直接读写该 Frame,而此时之前的脏页还没有刷盘,Page 数据也没有读取到 Frame 中(Problem #2)。
1 | Problem #1 |
1 | Problem #2 |
所以需要在解锁 BPM 之前给 Frame 加独占锁,但是这样做需要调整代码结构来避免死锁,也就是把 BPM 级别的共享变量的更新都放在解锁 BPM 之前,从而避免之后再加锁 BPM。这里给 Frame 加锁不会像之前一样阻塞 BPM,因为此时的 Frame 不被任何 PageGuard 持有。如果 Page 在缓冲池中,设置 Replacer 相关的数据一定要持有 BPM 锁,因为淘汰时只会加 BPM 锁,要避免页面在淘汰之后立即被访问的情况。(特殊情况可以不加,但是要注意如何设置值)
1 | Problem #3 |
1 | Problem #4 |
这样还是有问题,就是淘汰的 Frame 在包含脏页刷盘时会解锁 BPM,而此时如果有线程获取该 Page,则会从磁盘读取到旧页面或者此时磁盘中没有该页面(如果该页面是 NewPage)。此时需要额外维护哈希表存储相关信息,使用额外的锁来保护,该锁需要在解锁 BPM 之前持有,否则依然会发生上述错误。如果当前读取的 Page 还没有完成刷盘,则直接从旧 Frame 复制到当前 Frame 中。可以发现使用这种解锁 BPM 的方案会有各种问题,这都是我上次实现时遇到过的,最后 QPS 从 3700+ 反向优化到 1000+。
1 | Problem #4 |
主要瓶颈在单个 BPM 独占锁,可以使用类似 Java 的 ConcurrentHashMap 的思路,将 BPM 锁拆分成多个锁。由于不能使用外部现有的并发库,那么可以使用哈希表数组,根据 Page 的编号映射到不同哈希表中。如果需要同时锁定多个分区,则需要按照顺序加锁来避免死锁,可以使用 std::scoped_lock。还有很多坑点和方案一类似,最后 QPS 从 3700+ 反向优化到 900+。
1 | Problem #1 |
可以不使用额外的锁,而是设置标志位表示该页面正在刷盘或者读取中,例如在 Page 到 Frame 的哈希表中记录无效的 Frame 编号,然后其他获取线程使用条件变量等待执行完成。需要注意等待的条件是哈希表中不存在该 Page 映射或者对应 Frame 编号有效,因为如果空闲列表为空且无法淘汰其他 Frame,则需要手动删除该临时键值对而不会设置有效的 Frame 编号。此时可以在磁盘 I/O 时解锁 BPM,之后加锁修改标志位,然后唤醒线程。
如果磁盘调度器不使用线程池,则 QPS 反向优化到 900+。如果使用单队列 + 8 线程,则 QPS 优化到 5300+。实际上不使用磁盘调度器的后台线程,而是直接调用 Schedule 方法,QPS 可以到 14700+。使用单队列 + 16 线程,则 QPS 优化到 14000+,因为工作线程总共有 16 个。
如果为每个线程分配一个队列,任务循环放置到每个队列,则 QPS 只有 11000+。有延迟场景性能更低可能是因为没有任务窃取机制,某个线程没被调度导致相应队列的任务积压。但是无延迟场景的 QPS 更接近不使用后台线程的情况,因为各个线程不必竞争相同队列的锁。(该优化会有问题,如果存在对同一页面的多个磁盘 I/O 请求,可以想到的情况是主动 Flush 脏页,会存在多个对相同页面的写请求,无法保证顺序)
由于测试使用 8 个 Scan 线程顺序读,8 个 Get 线程随机写(使用 Zipfian 分布)。由于第三个测试结果的权值最大,主要优化第三个场景,也就是顺序读每 0.1ms 执行一次,随机写每 1ms 执行一次。理论上最大 QPS 是 88000,目前看来 Scan 操作的 QPS 优化空间较大。
1 | scan_qps_large / 1000 + get_qps_large / 1000 + scan_qps_small / 1000 + get_qps_small / 1000 + scan_qps_1ms + get_qps_1ms |
经过测试,Scan 操作的缓存命中率都是 0%,使用优先淘汰策略(不论优先淘汰什么类型)的 Scan 操作 QPS 可以提升到 30000+。使用默认的 LRUK 淘汰策略、优先淘汰只被 Scan 访问的 Frame、优先淘汰只被 Get 访问的 Frame 的 Get 操作命中率和 QPS 分别是 7% 5800+、11% 4300+ 和 3% 6500+。
虽然按理说优先淘汰只被 Scan 访问的 Frame 比较正常,因为 Scan 线程是顺序读本身就无法利用缓存,提前淘汰不会影响性能。基于单队列 + 16 线程的代码,可以将 QPS 从 14000+ 优化到 42000+。但是实际上优先淘汰任意访问类型的 Frame 都可以得到差不多的 QPS,因为只要提升 Evict 的速度,就可以大幅提升 Scan 操作的 QPS。另外,命中率更高的 Get 操作 QPS 反而更低,真不知道什么原因。
| Rank | Submission Name | scan_qps_large | get_qps_large | scan_qps_small | get_qps_small | scan_qps_1ms | get_qps_1ms | QPS |
|---|---|---|---|---|---|---|---|---|
| 98 | ALEX | 41513 | 4156 | 48125 | 643 | 3433 | 248 | 3776 |
| 24 | ALEX | 19407 | 19844 | 17793 | 21289 | 2491 | 2788 | 5358 |
| 16 | ALEX | 107110 | 104764 | 99692 | 102739 | 8370 | 5930 | 14715 |
| 18 | ALEX | 13775 | 13869 | 14001 | 16822 | 8148 | 5829 | 14035 |
| 22 | ALEX | 70177 | 70478 | 65910 | 73478 | 5775 | 5049 | 11105 |
| 4 | ALEX | 19866 | 10945 | 20708 | 13994 | 37939 | 4325 | 42330 |
参考 Documentation,Confluence,Docker,《Kafka 权威指南》,Kafka 101。TODO:消息传递语义(生产者、消费者角度)、日志存储/压缩方式。
参考 Install Docker Engine on CentOS,Image Mirror,DockerHub Apache Kafka。
1 | awk -F '=' '/PRETTY_NAME/ { print $2 }' /etc/os-release |
1 | 配置 Docker 软件仓库 |
1 | docker ps -a |
1 | docker pull apache/kafka |
在 CMU 15-445 中提到,DBMS 总是希望自己控制缓存,因为它可以根据查询负载灵活地实现优化策略,此时需要使用直接 I/O 绕过操作系统页面缓存避免冗余副本。而操作系统不知道这些,所以不建议使用 mmap 创建内存映射,来利用操作系统的缓存机制。例如,MongoDB 的默认存储引擎就从 MMAPv1 改为 WiredTiger。MySQL 的 innodb_flush_method 默认是 O_DIRECT(如果系统不支持则是 fsync),而 PostgreSQL 会使用操作系统缓存。
区分直接 I/O 和 fsync 刷盘,即使使用直接 I/O 数据也会写到磁盘缓冲区,结合刷盘才能保证持久化。另外,如果在持久化页面的过程中崩溃,需要恢复损坏的页面数据(当数据库页面大于硬件页面时,读写不具备原子性),MySQL 使用 Doublewrite Buffer 来恢复数据,而 PostgreSQL 使用 WAL 和 Full Page Write 保证恢复数据。
而 Kafka 在很大程度上依赖文件系统来存储和缓存消息。Kafka 使用 Java 开发,对象的内存开销较大(对象头的固定开销),堆中数据增加使得垃圾收集的时间更长,所以 Kafka 不在堆中维护缓存而是使用操作系统的页面缓存。
使用操作系统的页面缓存有如下优点:① 缓存可以使用所有空闲内存而不受限于 JVM 堆内存,使用字节结构紧凑存储数据而不是使用对象可以高效利用空间,并且不会受到 GC 惩罚(因为缓存由操作系统管理)。 ② 重启 Kafka 进程不会清空操作系统缓存,而在堆中维护缓存,在重启时需要缓存重建(冷启动)。③ 操作系统使用预取和批量读写来提升磁盘操作的性能,顺序磁盘访问在某些情况下比随机内存访问更快。
在缓存大小固定的情况下,B 树的性能随着数据量的增加而降低,由于磁盘寻道的开销较大,性能降低的程度也更大(缓存未命中)。Kafka 将队列持久化到单个文件中,使用顺序读和追加写,且读写操作不会相互阻塞。因为操作的性能和数据量的大小无关,所以服务器可以使用多个廉价的、低转速的磁盘,带来的额外好处是可以将消息保留相对较长的时间,而不是在消息被消费之后立即删除。
由于顺序读和追加写的磁盘访问模式,大型读写的效率在可接受的范围内。目前系统低效的原因有两个,太多小型 I/O 操作和过多的字节复制。解决方案是使用批量 I/O,使用生产者、代理和消费者共享的标准二进制消息格式(因此数据块可以在它们之间传输而无需修改),以及零拷贝技术。(推荐阅读 Efficient data transfer through zero copy)
将数据从文件传输到套接字的常规路径:① 操作系统将数据从磁盘读取到内核空间的页面缓存;② 应用程序将数据从内核空间的页面缓存读取到用户空间的缓冲区;③ 应用程序将数据写回到内核空间的套接字缓冲区;④ 操作系统将数据从套接字缓冲区复制到网卡缓冲区,然后通过网络发送。
总共需要四次数据复制和两次系统调用,①④ 是使用 DMA 复制,②③ 是使用 CPU 复制。sendfile 系统调用的作用是,将数据从一个文件描述符传输到另一个文件描述符。使用该系统调用,可以绕过用户空间,直接将数据从内核空间的页面缓存复制到套接字缓冲区(CPU 复制)。如果网卡支持收集操作且 Linux 内核是 2.4 及更高版本,那么就可以消除唯一的 CPU 复制,数据直接从内核空间的页面缓存传输到网卡缓冲区,从而实现零拷贝(不需要 CPU 参与复制,所以被称为零拷贝)。
零拷贝允许操作系统将数据从页面缓存直接发送到网卡缓冲区,总共需要两次数据复制和一次系统调用。当一个主题被多个消费者消费时,数据只被复制到页面缓存中一次,然后在每次消费时重复使用,而不会在每次消费时都复制到用户空间,这允许消息以接近网络连接限制的速率被消费。TLS/SSL 库在用户空间运行,内核中的 SSL_sendfile 目前 Kafka 不支持,所以启用 SSL 时不会使用 sendfile。
在某些情况下,瓶颈实际上不是 CPU 或磁盘,而是网络带宽。Kafka 使用批量压缩(而不是压缩单个消息,因为冗余通常是由于相同类型的消息之间的重复,这样可以提供更好的压缩比),生产者将一组消息压缩发送给服务器,代理解压缩来验证完整性,然后依然以压缩格式存储到磁盘(日志文件中)和发送给消费者。Kafka 支持 GZIP、Snappy、LZ4 和 ZStandard 压缩协议,更多细节见 Compression。
在 KRaft 模式下,每个 Kafka 服务器都可以使用 process.roles 属性配置为控制器、代理,或者同时充当控制器和代理。同时充当控制器和代理的 Kafka 服务器被称为组合服务器,组合服务器更易于操作,但是将控制器和代理耦合。例如,在组合模式下,不能将控制器与代理分开滚动升级或扩展,所以在关键部署环境中不建议使用组合模式。
控制器负责存储 Kafka 集群的元数据信息,使用 Raft 协议实现容错。Kafka 集群中的所有服务器都使用 controller.quorum.bootstrap.servers 属性(使用动态仲裁时设置该属性,类似生产者的 bootstrap.servers 属性,不需要包含所有控制器,静态仲裁使用 controller.quorum.voters 属性)来发现控制器,每个控制器使用 host 和 port 唯一标识。控制器可以向代理推送元数据,或者代理向控制器拉取元数据,从而所有 Kafka 节点都可以响应生产者对元数据的请求。
生产者首先会向 bootstrap.servers 列表中的代理发送元数据请求,来定位分区的领导者代理,然后将数据发送给该领导者代理。如果生产者没有指定分区或者键,则将数据轮询发送到主题下的各个分区。否则,将数据发送到对应的分区。
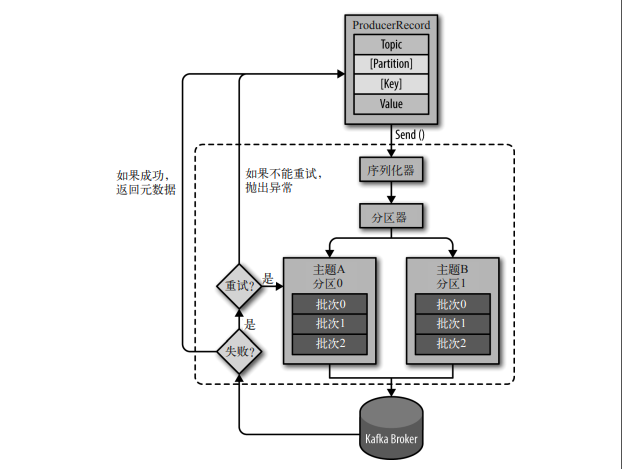
min.insync.replicas 表示 ISR 的最小数量(默认 1)。acks 参数表示生产者发送的请求返回之前要求同步的副本数(默认 all)。acks=0 表示不等待服务器的响应直接返回(此时重试配置不生效),acks=1 表示领导者将记录存储到本地日志就返回响应,acks=all 表示领导者等待 ISR 中的所有副本确认之后才返回响应(和 acks=-1 等价),此时 ISR 数量需要满足 min.insync.replicas,否则代理将拒绝该分区的写入操作。注意这里是向生产者返回响应,在消息被复制到所有 ISR 且满足 min.insync.replicas 之前,该消息对消费者是不可见的。
max.in.flight.requests.per.connection 参数表示生产者在单个连接上发送的未确认请求的最大数量(默认 5)。如果此配置设置为大于 1 并且不启用幂等性,则在请求失败后存在消息重新排序的风险(由于重试请求)。如果禁用重试或者启用幂等性,将可以保证单分区内消息的顺序(在代理中按照生产顺序排列)。此外,启用幂等性要求此配置的值小于等于 5,因为代理最多只缓存每个生产者最后 5 个请求的元数据。代理根据生产者编号(PID)、分区编号、分区内的自增序列号对消息去重,生产者重新连接到代理会被分配新的 PID(不使用事务时),所以幂等性不保证跨会话去重。
enable.idempotence 参数表示生产者是否保证每条消息只在流中写入一次(默认 true)。启用幂等性要求 max.in.flight.requests.per.connection <= 5,retries > 0,ack=all。retries 参数表示重试次数(默认 2147483647 次),如果 delivery.timeout.ms 超时,则会请求会直接失败而不会再重试。
delivery.timeout.ms 参数表示调用 send() 返回后,报告成功或失败的时间上限(默认 2 min)。包括发送的延迟时间(由 linger.ms 指定)、代理确认的时间(由 acks 指定是否需要确认)以及重试的时间。此配置的值应大于等于 request.timeout.ms 和 linger.ms 之和。
batch.size 参数表示单个批次能够使用的内存大小(默认 16 KB),不同分区的消息被放到不同的批次中。linger.ms 参数表示发送的延迟时间(默认 5 ms),当数据占用内存或者等待时间到达上限,就会将数据发送给代理。max.request.size 表示请求的大小上限(默认 1 MB),代理对请求大小也有限制(message.max.bytes),所以生产者的配置要和代理匹配。buffer.memory 表示生产者缓存消息的缓冲区大小(默认 32 MB)。
partitioner.class 分区器确定消息应该发送到主题的哪个分区(默认值 null)。如果未设置则使用默认的分区逻辑,首先根据指定的分区或者键的哈希值选择分区,否则选择粘性分区(stick partition),此策略会将记录发送到一个随机分区,直到向该分区发送至少 batch.size 字节的数据,再随机选择和当前分区不同的分区。如果设置 RoundRobinPartitioner 分区策略,则轮询发送到不同的分区(该策略存在问题,详细见文档)。或者实现指定接口来自定义分区器。
复制的基本单位是主题分区,由一个 Leader 和零个或多个 Follower 组成,所有写入操作发送到该分区的 Leader,读取操作可以发送到 Leader 或 Follower。通常分区的数量多于代理的数量,Leader 均匀分布在代理之间。Follower 会像普通的消费者一样从 Leader 拉取消息(批量拉取),将其应用到日志中。
分区的 Leader 会维护同步副本的集合(in sync replicas,ISR),只有 Follower 和 Controller 保持联系(由 broker.session.timeout.ms 配置),且 Follower 没有落后 Leader 很多(由 replica.lag.time.max.ms 配置),该 Follower 才会在 ISR 中。当分区中的所有 ISR 将消息应用到日志时,该消息被视为已提交,且 ISR 的数量满足 min.insync.replicas 时,该消息才对消费者可见(类似 Raft 复制到多数上才提交日志然后应用到状态机)。Kafka 提供的保证是,只要至少有一个同步副本存活,那么已提交的消息就不会丢失。
多数复制策略在有 \(2f+1\) 节点时可以容忍 \(f\) 个节点故障,优点是延迟时间取决于速度最更快的 \(f+1\) 个服务器,而不是速度更慢的剩余 \(f\) 个服务器,缺点是磁盘空间变为 \(2f+1\) 倍和吞吐量变为 \(\frac{1}{2f+1}\)(相比不使用复制而言)。所以多数策略更常出现在共享集群配置中而在数据存储中不常见。
Kafka 使用的不是多数策略而是动态维护 ISR,ISR 中的节点会和 Leader 保持同步,只有该集合中的节点才有资格参与选举。每当 ISR 集合发生变化时,该集合都会被持久化到集群元数据中(存储到 Controller 服务器)。Kafka 使用 ISR 模型和 \(f+1\) 个节点,可以容忍 \(f\) 个节点故障而不会丢失已提交的消息。相比多数策略优缺点正好相反,由于复制因子更低,所以磁盘空间和吞吐量更优。而且客户端可以选择是否等待消息提交(使用 acks 配置),从而改善等待最慢服务器同步导致的提交延迟。
许多复制算法都依赖于稳定存储,如果存储发生故障会导致潜在的一致性问题。但是稳定存储假设存在两个问题,首先存储系统中最常见的就是磁盘错误,其次每次写入操作都需要使用 fsync 保证一致性会使性能下降两到三个数量级。Kafka 不要求崩溃节点在恢复时能完整保留所有数据(缓存中的数据丢失),并且确保副本在重新加入 ISR 时已经重新同步。
如果复制某个分区的所有节点都停止运行,有两种处理方式,主要是在一致性和可用性之间权衡。Kafka 默认等待 ISR 中的一个副本恢复运行,然后将其作为 Leader(希望它仍保存着所有数据)。或者也可以选择最先恢复运行的副本作为 Leader,该副本不一定在 ISR 中,不保证包含所有已提交消息。
一个 Kafka 集群包含成百上千的分区,分区和 Leader 在代理中尽可能均匀分布以平衡负载。节点故障需要为将该节点作为 Leader 的所有分区重新选举 Leader,选举过程中的分区不可用。Controller 负责管理代理的注册,如果 Controller 检测到代理故障,会从 ISR 的剩余节点中选举出 Leader,这允许批量处理多个分区的选举而不是每个分区单独选举,从而减少不可用的时间。
group.consumer.heartbeat.interval.ms 表示消费者和组协调器的心跳间隔时间(默认 5 s)。
group.consumer.session.timeout.ms 表示组协调器判断消费者故障的超时时间(默认 45 s)。
group.consumer.assignors 表示支持的消费者组的分区分配器列表(默认 uniform、range),默认使用列表中的第一个分配器。
Kafka 消费者通过向其想要消费的分区的领导者代理发出获取请求来工作,消费者在每次请求中指定日志偏移量,可以修改偏移量实现重复消费。生产者将数据推送给代理,消费者从代理拉取数据。数据由消费者拉取而不是由代理推送,从而消费者可以根据自身消费能力来拉取数据,且可以批量拉取来提升吞吐量。当代理中没有数据时,Kafka 使用长轮询来减少频繁轮询的忙等待开销。消费者在长轮询中阻塞,直到给定字节的数据到达。
如何确认消息是否被消费?假设代理等待消费者发送确认消费的请求,但是如果消费者在消费消息之后、发送确认之前崩溃,那么消息将被消费两次。由于每个分区只会被每个订阅该主题的消费者组中的一个消费者消费,所以可以为每个消费者组的每个分区维护一个日志偏移量,从而避免代理维护消息状态的复杂性。如果消费者在处理完消息、提交偏移量之前崩溃,那么新的消费者会重复消费该消息。
Kafka 会使用名为 __consumer_offsets 的特殊压缩主题来存储日志偏移量消息,根据消费者组的名称将消费者组分配到该主题的不同分区,该分区的领导者代理被称为该消费者组的组协调器(group coordinator),消费者可以通过向任何 Kafka 代理发出 FindCoordinatorRequest 请求来发现组协调器。Kafka 消费者会跟踪它在每个分区的日志偏移量,并且能够向组协调器(group coordinator)提交、获取偏移量。
当组协调器收到 OffsetCommitRequest 请求时,它会将偏移量记录到 __consumer_offsets 主题的指定分区,只有当该分区的所有副本都确认之后,组协调器才会返回响应。如果偏移量在超时时间内无法复制到所有副本,偏移量将提交失败,消费者可以重试提交。代理会定期压缩该主题,因为只需要维护每个分区最近提交的偏移量。组协调器会将偏移量缓存在内存中,以便快速向消费者提供偏移量信息。
fetch.min.bytes 表示获取请求返回的最小字节数(默认 1 B),fetch.max.bytes 表示获取请求返回的最大字节数(默认 50 MB)。remote.fetch.max.wait.ms/fetch.max.wait.ms 表示代理在响应远程/本地获取请求之前将等待的最大时间(默认 500 ms),如果数据到达下限或者请求超时则返回响应。max.partition.fetch.bytes 表示代理从每个分区返回的最大字节数(默认 1 MB)。
enable.auto.commit 表示是否定时提交偏移量(默认 true),auto.commit.interval.ms 定时提交的频率(默认 5 s)。
max.poll.interval.ms 表示使用消费者组管理时 poll 方法调用的最大间隔时间(默认 5 min)。如果超时之前未调用 poll 方法,该消费者将被视为故障,触发消费者组的重新平衡(将该消费者消费的分区分配给其他成员)。可以使用静态成员机制避免立即触发重新平衡,以提高程序的可用性,这可以通过为组成员(消费者)分配永久的标识符来实现(使用 group.instance.id 配置)。如果使用静态成员,超时不会立即重新平衡,消费者将会停止给组协调器发送心跳,在 session.timeout.ms (默认 45 s)超时之后才触发重新平衡。注意,如果使用新版重新平衡协议 KIP-848(默认不启用),session.timeout.ms 和 partition.assignment.strategy 配置将不可用。
partition.assignment.strategy 表示在消费者组中分配分区的策略,默认是 [RangeAssignor,CooperativeStickyAssignor],表示默认使用 RangeAssignor,允许在一次滚动升级之后将策略升级为 CooperativeStickyAssignor。RangeAssignor 基于主题分配分区,根据主题内分区数除以组内消费者数来均匀分配,如果有余数则从前往后依次分配,多主题分区的余数分配会导致负载倾斜。RoundRobinAssignor 轮询分配分区,StickyAssignor 保留现有分配的情况下尽可能实现负载均衡,CooperativeStickyAssignor 保留现有分配的情况下尽可能实现负载均衡,且允许未受影响的分区在重新平衡时继续消费。允许实现 ConsumerPartitionAssignor 接口来自定义分配策略。
auto.offset.reset 表示当在 Kafka 中没有初始偏移量或者服务器上的当前偏移量不存在时(由于数据被删除),应该从什么偏移量开始消费。latest 表示设置为最新偏移量(默认),当新增分区数量时存在丢失消息的风险,如果生产者在消费者重置偏移量之前就向新分区发送消息。earliest 表示设置为最早偏移量,none 抛出异常,by_duration:<duration> 表示设置为消费过去一段时间的数据。