ZooKeeper: Wait-free coordination for Internet-scale systems
阅读论文 ZooKeeper,参考 FAQ,note,官方文档,另一个课程的 note。
概述
ZooKeeper 是一个协调服务,用于协调分布式应用程序。它没有实现特定的协调原语(例如:配置、选举、锁),而是提供 API 供应用程序开发者使用,让开发者根据实际需要实现协调原语。ZooKeeper API 具有无等待特性,提供事件驱动机制。ZooKeeper 使用流水线(pipeline)架构处理请求,流水线自动支持客户端请求的 FIFO 执行顺序,从而允许客户端异步发送请求。ZooKeeper 没有实现可线性化一致性模型,它仅保证写操作的异步可线性化,以及读操作的写后读和单调读一致性(术语取自 DDIA),适合读多写少的工作负载。
会话
客户端在连接到服务器时建立一个会话(session),同时获得一个会话 ID。只要会话 ID 有效,应用程序就可以通过客户端调用 ZooKeeper API。客户端会定期向服务器发送心跳,如果服务器在超时时间内没有收到心跳,则服务器会结束会话。如果客户端当前连接的服务器故障,则客户端在会话 ID 过期之前自动尝试连接到另一台服务器。
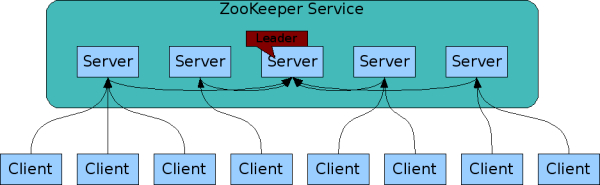
PS:创建会话类似写操作,需要经过多数服务器同意,会话的状态也会使用日志持久化,它是一个全局会话。这也可以解释,为什么客户端可以使用同一个会话 ID 透明地切换到另一台服务器。由于开销较大,ZooKeeper 在之后的版本添加了本地会话功能,本地会话只能执行全局会话操作的子集,状态只在本地服务器维护。
数据模型和监视
ZooKeeper 以类似文件系统的树形结构在内存中存储协调数据(应用程序元数据),树中的数据节点被称为 znode,由路径名唯一标识。不同的应用程序在各自的子树中组织数据,存储在节点中的数据以原子的方式被读写。节点会维护一个统计结构,包含版本号、时间戳和事务 ID(zxid)等元数据。节点分为常规(Regular)和临时(Ephemeral)两种类型,客户端可以显示创建和删除节点。特别的,临时节点如果没有被显示删除,则在创建它们的会话终止时被自动删除,以及临时节点不能有子节点。
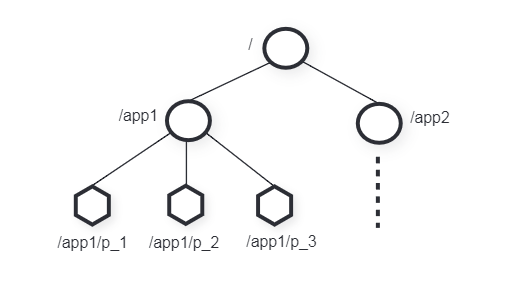
创建节点时,客户端可以设置顺序(sequential)标志,从而将一个计数值附加到该节点的路径末尾,同一父节点的子节点的计数值根据创建顺序单调递增。客户端可以为节点设置一次性监视(watch)标志,该标志在客户端连接的服务器本地维护。当监视触发时,服务器会向客户端发送一个监视事件,同时取消监视。有两种监视类型,监视数据和监视子节点。有四种监视事件,创建、删除、数据变化、子节点变化(不包含子节点的数据变化)。监视和会话相关,当会话结束时,监视也会被取消。ZooKeeper 保证设置监视的客户端在看到变化之前,会收到服务器的通知。会话事件也会触发监视,以便客户端知道监视事件可能延迟。
原语示例
客户端可以使用 ZooKeeper API 实现更强的原语,示例如下。更多示例(双重屏障、2PC、选举)可以查看官方文档。
配置管理
ZooKeeper 可用于分布式应用程序的配置管理,可以将配置存储在 znode 中。客户端从 znode 读取配置,同时设置监视标志。如果配置被更新,则客户端会收到通知,然后再次从该 znode 读取配置和设置监视标志。
群组成员
客户端可以创建一个 znode 表示一个群组,当进程以该群组的成员身份启动时,它会在该 znode 下创建一个临时子 znode。如果每个进程有一个唯一的名称,则将该标识作为子 znode 的名称,否则可以使用顺序标志,使其获得唯一的名称。进程可以将其元数据存储在该子 znode 中,例如地址和端口。如果进程终止,则临时节点会被自动删除。可以通过在 znode 上设置监视标志,从而监视群组成员的变化。
简单锁
可以将一个指定路径的 znode 作为锁,客户端可以创建临时 znode 来获取锁,其他客户端通过判断 znode 是否存在来判断是否能够获取锁,同时设置监视标志。当临时 znode 被显示或自动删除,则表示锁被释放。此时,等待锁的客户端将收到通知。但是该实现存在羊群效应(herd effect):在锁被释放时,许多客户端会争抢同一个锁。
无羊群效应的简单锁
直觉上来说,将获取锁的请求按照 FIFO 的顺序排队处理,那么就可以避免羊群效应。可以使用顺序标志在指定父 znode 下创建临时子 znode,客户端通过判断其创建的临时 znode 是否是序号最小的,来判断它是否已获取锁。当客户端需要释放锁时,只需删除其创建的临时 znode。个人认为,有无羊群效应的简单锁,有点像是 notify_all 和 notify_one 的区别。

特别的,在代码实现时有一个陷阱,ZooKeeper 没有提供监视来通知当前 znode 的序号是否最小。在创建 znode 之后, 我们首先需要获取子 znode 列表,判断当前是否是最小的。如果不是,则可以在前一个节点上设置监视。但是,该监视触发并不意味着当前客户端已获取锁,因为有可能只是前一个客户端提前结束会话,此时仍存在更小的序号。
读写锁

实现细节
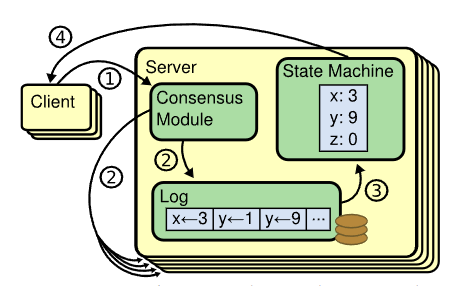
ZooKeeper 使用复制提供容错,使用原子广播协议(ZAB)保证多个副本之间的一致性。客户端仅连接到一个服务器发送请求,写请求会被转发给领导者,读请求读取本地数据库而不需要通过领导者。本地处理读请求使得读取性能可以随着服务器的数量增加而增加,而不会受限于单个领导者。复制数据库是一个内存数据库,当日志持久化到磁盘时,才会将日志应用到内存数据库,同时会定期为数据库生成快照。PS:类似 Raft,内存数据库实际上就是一个状态机。
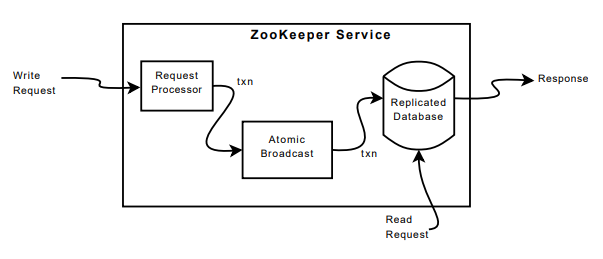
ZooKeeper 使用 ZAB 保证写操作的可线性化,同时保证异步请求按照客户端 FIFO 的顺序执行,从而实现写操作的异步可线性化(A-linearizability)。当领导者收到写请求时,如果请求包含的版本号和目标 znode 的未来版本号匹配,就会将请求转换为事务。之所以要和未来版本号匹配,是因为可能存在尚未应用到数据库的事务。如果事务未提交(复制到大多数),则无法应用到数据库。ZooKeeper 保证事务是幂等的,〈transactionType, path, value, new-version〉。
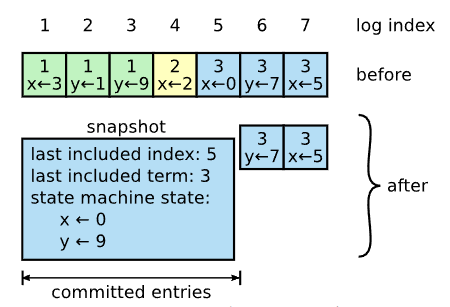
ZooKeeper 使用的是模糊快照(fuzzy snapshot),因为允许在创建快照的过程中更改状态机,而且也不像 Raft 使用写时复制,所以快照不对应某个时刻的状态,故称为模糊快照。不过,由于事务的幂等性,重放相同的日志也没有关系。从日志的角度看,模糊快照并不对应一个连续的日志范围,可能是断断续续的。
客户端向服务器发送读写请求和心跳消息,得到的响应中会包含服务器的 zxid。如果客户端连接到新服务器,会检查客户端的 zxid 和新服务器的 zxid,确保新服务器满足客户端的单调读一致性。如果新服务器的视图更旧,客户端可以连接另一台服务器。
问题
Q:无等待(wait-free)是什么意思?
A:论文 Wait-Free Synchronization 进行了介绍,并发数据对象的无等待实现可以保证,任何进程都能在有限步中完成任何操作,而不论其他进程的执行速度如何。个人认为这个定义有点抽象,无等待还有一个层次结构和共识数。类似的术语还有无锁、无障碍、无阻塞。FAQ 提供了一个简单的解释,为什么 ZooKeeper 是无等待的,因为客户端调用 API 不会被其他客户端阻塞,ZooKeeper 没有使用锁来阻塞调用。
Q:为何流水线自动支持客户端请求的 FIFO 执行顺序?异步请求为何能提高性能?
A:我的理解是 TCP 可以保证客户端请求的 FIFO 到达顺序。流水线将一个处理过程分解为多个组件,能够充分利用系统的资源。但流水线依然是一个顺序的处理过程,一般就是按照到达顺序处理的,所以能够自动支持 FIFO 执行顺序。异步请求能提高性能是流水线的特性,如果同步发送请求,流水线中的很多组件会处于空闲状态。
FAQ 中有问到 ZooKeeper 如何实现异步请求的 FIFO 执行顺序,按照论文的逻辑,这个问题就不对。论文首先说流水线支持 FIFO 执行顺序,然后推出客户端可以发送异步请求。从而我觉得,FAQ 的答案也不对。FAQ 对流水线的解释也有问题,他把流水线解释为批处理。
Q:如何实现读操作的写后读和单调读一致性?
A:写后读一致性可以由客户端的 FIFO 执行顺序保证,而单调读一致性通过检查客户端和服务器的 zxid 保证。
Q:ZooKeeper 如何实现监视(watch)?
A:FAQ 有解释,客户端通常会注册一个回调函数,该函数在监视触发时调用。Go 使用通道(channel)来实现,当监视触发时,服务器会向通道发送一个事件,然后应用程序可以从通道中获取该事件。但是有个疑问,Go 的通道能跨网络传输数据么。
Q:为什么请求不幂等,而事务幂等?
A:假设有一个带顺序标志的创建节点的请求,那么多次发送请求会创建不同的节点。事务是请求的幂等形式,论文中提到形如 〈transactionType, path, value, new-version〉。
Q:ZooKeeper 服务器、客户端和应用程序的关系?
A:个人理解,服务器提供低级原语,客户端使用 API 实现更高级的原语,应用程序使用客户端提供的高级原语。
Q:ZooKeeper 中的 zxid 和版本号有什么关系?
A:ZooKeeper 的每次状态更改(写操作)都会递增 zxid,而版本号则是 znode 的属性。个人认为,zxid 是 ZAB 层面的,版本号是数据库(状态机)层面的。
Q:可线性化和可串行化的区别?
A:可以看下 Linearizability versus Serializability,很清晰。
总结
刚开始看这篇论文,涉及很多没见过的术语,看着比较折磨。如果深入细节的话,会花费很多时间。我确实一开始没有抓住重点,陷入如何在代码层面使用 ZooKeeper,无等待和通用对象是什么意思之类的。但是,如果从更高的层面来看,ZooKeeper 可以理解为 ZAB + 数据库(状态机),就是使用数据树结构提供一个通用的 API。
在查找资料的过程中发现很多不一致的地方,例如:API 文档中描述异步请求会排队等待发送,但按照论文的描述应该不是这样的,不然怎么提高性能;一致性保证中提到单一系统映像,定义首先说保证看到相同的视图,然后又说不会看到旧视图,但这完全不是一个意思;FAQ 中对异步请求如何实现客户端 FIFO 执行顺序的讨论,我认为论文和另一份笔记都证明 FAQ 的错误。
在阅读论文和资料的过程中,经常会看到某个描述,感觉模糊不清,只能凭自己的猜测去理解。实际上确实有很多模糊的地方,没有描述具体的实现方式,但有些问题其实论文中也给出了回答。所以,在读论文的过程中还是要仔细一点,遇到不懂的不要随便猜测,先记下问题,因为很可能是一个错误的猜测,还会干扰之后的理解。总之,论文只是提供一个简要的说明,深入理解还需要实际使用 ZooKeeper,以及阅读源码。